Jerarquía de operaciones
Una expresión con operaciones combinadas es una expresión en la que deben realizarse cálculos matemáticos como la suma, la resta, el producto, la división y/o el cálculo de una potencia.
Estas operaciones pueden implicar números reales, pero para facilitar la comprensión, en este artículo sólo se utilizarán números enteros.
A continuación se presentan dos expresiones con diferentes operaciones combinadas:
5+7×8-3
(5+7)x(8-3).
Las expresiones anteriores contienen los mismos números y las mismas operaciones. Sin embargo, si se hacen los cálculos los resultados serán diferentes. Esto se debe a los paréntesis que tiene la segunda expresión y a la jerarquía con la que debe resolverse la primera.
Clave para desarrollar la jerarquía de operaciones
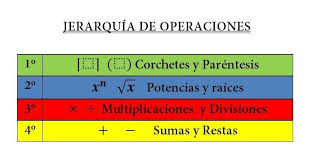
Cuando hay símbolos de agrupación como paréntesis (), paréntesis [] o teclas {}, siempre se debe resolver primero lo que hay dentro de cada par de símbolos.
En el caso de que no haya símbolos de agrupación, la jerarquía es la siguiente:
- resolver primero las potencias (si las hay)
- entonces los productos y/o divisiones (si las hay) se resuelven
- por último se resuelven las sumas y/o restas
Ejercicios de jerarquía de operaciones para resolver
Ejercicio
Resuelva las dos operaciones presentadas anteriormente: 5+7×8-3 y (5+7)x(8-3).
Solución
Como la primera expresión no tiene signos de agrupación, debe seguirse la jerarquía descrita anteriormente, por lo tanto, 5+ 7×8- 3 = 5+56-3=58.
Por otro lado, la segunda expresión tiene signos de agrupamiento, por lo que primero se debe resolver qué hay dentro de esos signos y por lo tanto, (5+7)x(8-3)=(12)x(5)=60.
Como se ha dicho antes, los resultados son diferentes.
Contenido