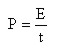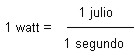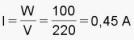Fórmula de potencia eléctrica

Potencia eléctrica

Potencia es la velocidad a la que se consume la energía.

También se puede definir Potencia como la energía desarrollada o consumida en una unidad de tiempo, expresada en la fórmula

Potencia es igual a la energía dividido por el tiempo

Si la unidad de potencia (P) es el watt (W), en honor de Santiago Watt, la energía (E) se expresa en julios (J)  y el tiempo (t) lo expresamos en segundos, tenemos que:

Entonces, podemos decir que la potencia se mide en julio (joule) dividida por segundo (J/sec) y se representa con la letra "P".

Además, diremos que la unidad de medida de la potencia eléctrica "P" es el "vatio", y se representa por la letra "W".

Como un J/segundo es equivalente a 1 vatio ( W ), por lo tanto, cuando se consume 1 julio de energía en un segundo, estamos gastando o consumiendo 1 vatio de energía eléctrica.

Para entender esto, hagamos un símil: Si la energía fuera un líquido, la potencia sería los litros por segundo vertidos por el tanque que lo contiene.

Cálculo de la potencia

Para calcular la potencia consumida por un dispositivo conectado a un circuito eléctrico, el valor del voltaje, en voltios (V) , aplicado se multiplica por el valor de la corriente (I) que fluye a través de él (expresado en amperios ).

La siguiente fórmula se utiliza para hacer este cálculo matemático:

P = V • I

Expresado en palabras: La potencia (P) es igual al voltaje (V) multiplicado por la intensidad (I).

Como la potencia se expresa en vatios (W), sustituimos la "P" que identifica la potencia por su equivalente, es decir, la "W" de vatio, también tenemos eso: P = W , por lo tanto,

W = V • I

Expresado en palabras: Vatio (W) es igual al voltaje (V) multiplicado por la intensidad (I).

Si conocemos la potencia en vatios de un dispositivo y el voltaje aplicado (V) y queremos encontrar la corriente (I) que fluye a través de un circuito, aclaramos la fórmula anterior y realizamos la operación matemática correspondiente:

Si observamos la fórmula W = V - I veremos que el voltaje y la intensidad de la corriente que fluye a través de un circuito eléctrico son directamente proporcionales a la potencia; es decir, si uno de ellos aumenta o disminuye su valor, la potencia también aumenta o disminuye proporcionalmente.

Entonces podemos deducir que, 1 vatio ( W ) es igual a 1 amperio de corriente ( I ) que fluye por un circuito, multiplicado por 1 voltio ( V ) de tensión o voltaje aplicado.

Ejemplo de potencia eléctrica

¿Cuál será la potencia o el consumo en vatios de una bombilla conectada a una red eléctrica doméstica monofásica de 220 voltios, si la corriente que circula por el circuito de la bombilla es de 0,45 amperios?

Sustituyendo los valores de la fórmula que tenemos:

P = V • I
P = 220 • 0,45
P = 100 watt

Es decir, el consumo de energía de la bombilla será de 100 W.

Si, en el mismo ejemplo, quisiéramos encontrar la intensidad de la corriente que fluye a través de la bombilla y conocemos la potencia y el voltaje o tensión aplicada al circuito, usamos la fórmula

Si realizamos la operación utilizando los mismos datos del ejemplo anterior, tendremos:

o

Para encontrar el consumo de energía en vatios de un dispositivo, también se puede utilizar cualquiera de las dos fórmulas siguientes:

Con la primera, el valor de la potencia se obtiene cuadrando el valor de la corriente en amperios (A) que fluye a través del circuito, y luego multiplicando este resultado por el valor de la resistencia en ohmio u ohmio (Ω) de la carga o consumidor conectado al propio circuito.