Recta tangente y recta normal a una curva en un punto

Se dice que una línea es tangente a una función en un punto cuando pasa por ese punto y su pendiente es f'(a). La recta normal a una función en un punto, por otro lado, es la que pasa por ese punto y tiene una pendiente -1/f'(a).

Tangente (geometría)

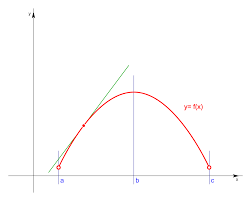
La tangente a una curva en un punto P es una línea que toca la curva sólo en ese punto, llamado el punto tangente. Se puede decir que la tangente forma un ángulo nulo con la curva en las proximidades de ese punto. Esta noción puede generalizarse desde la línea tangente a un círculo o una curva a las figuras tangentes en dos dimensiones -es decir, figuras geométricas con un solo punto de contacto (por ejemplo, la circunferencia inscrita)-, a los espacios tangentes, donde el concepto de tangencia se clasifica en más dimensiones.

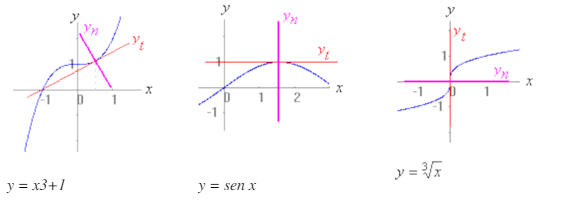
Recta tangente y normal

Una recta se define cuando conocemos dos puntos por los que pasa, pero también cuando conocemos un punto por el que pasa y la pendiente de la misma. En este caso, el punto, común a ambos, es (a,f(a)). Para el cálculo de las pendientes (f'(a) y -1/f'(a) respectivamente) es imprescindible conocer el valor de la derivada de la función en el punto.

Expresión de la recta tangente

La recta tangente a una función en un punto de abscisas x=a se define como la recta que pasa por (a,f(a)) y tiene como pendiente la derivada de la función en el punto, f'(a). Su expresión es

y-f(a)=f'(a)⋅(x-a)

Expresión de la recta normal

La línea normal de una función en un punto x=una abscisa se define como la línea que es perpendicular a la línea tangente en ese punto. Por lo tanto, pasa por (a,f(a)) y tiene una pendiente de -1/f'(a). Su expresión es

Entrada Relacionada: Ejemplos de movimiento rectilíneo uniforme

y-f(a)=-1/f'(a)⋅(x-a)