Distribución normal
Suponiendo que X es un valor observado de una muestra (o población), con una media (o μ) y una desviación estándar s (o σ), el valor de x en unidades estándar -representado por z- se calcula restando la media del valor dado y dividiendo el resultado por la desviación estándar, y definido por la siguiente fórmula
En poblaciones:
En muestras de población:
La unidad estándar muestra el número de desviaciones estándar en que un valor determinado está por encima o por debajo de la media de su muestra o población. Entonces una unidad estándar de valor negativo está por debajo de la media, mientras que una unidad estándar de valor positivo está por encima de la media. Por consiguiente, para calcular una unidad estándar es necesario conocer previamente el valor de la media y la desviación estándar de la muestra o población.
Distribución normal ejercicios resueltos
Halla las siguientes probabilidades en una distribución N ( 0, 1 )
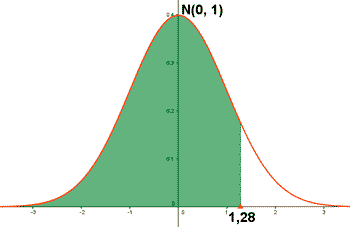
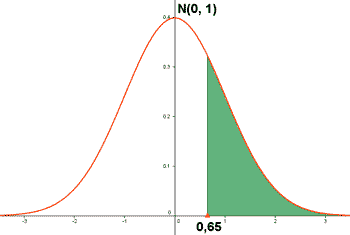
a) P (Z ≤ 1,28) b) P (Z ≥ 0,65)
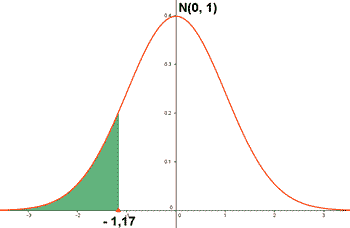
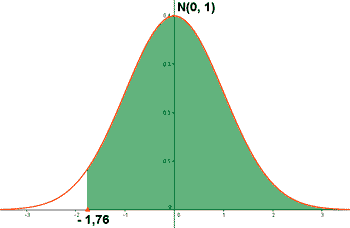
c) P (Z ≤ -1,17) d) P (Z ≥ -1,76)
a)
P ( Z ≤ 1,28 ) = 0,8997.
b)
P ( Z ≥ 0,65 ) = 1 - P ( Z ≤ 0,65 ) = 1 - 0,7422 = 0,2578.
c)
P ( Z ≤ -1,17 ) = P ( Z ≥ 1,17 ) = 1 - P ( Z ≤ 1,17 ) = =1 - 0,8790 = 0,121
d)
P ( Z ≥ -1,76 ) = P ( Z ≤ 1,76 ) = 0,9608
Contenido