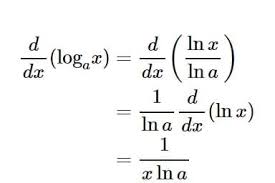
Cómo calcular logaritmos sin calculadora

Se dice que el matemático escocés John Neper, divulgó el concepto matemático llamado logaritmo aproximadamente en el año 1614, y determinó sus propiedades a partir de la relación existente entre las progresiones geométricas y aritméticas. Gracias al desarrollo de esta gran herramienta, Isaac Newton y Kepler pudieron acelerar su trabajo en el campo de la astronomía

DEFINICIÓN DE LOGARITMO

El logaritmo de un número con respecto a otra base llamada es el exponente al que debe elevarse la base para obtener ese número.

Así, por ejemplo, podemos mencionar que la base del logaritmo diez de mil es igual a tres, debido a que 10³=1000. La notación clásica para un logaritmo es:

PROPIEDADES DE LOS LOGARITMOS

CÁLCULO DE LOGARITMOS

Para calcular los logaritmos de los números reales, se puede presentar una amplia variedad de casos, que van de lo simple a lo complejo. A veces es necesario hacer uso de técnicas matemáticas avanzadas como las series de Taylor, el uso de calculadoras científicas o incluso la manipulación de tablas especiales. También hay casos en los que el logaritmo en una cierta base de un número real se calcula rápidamente mediante el uso del álgebra y las propiedades elementales, como puede verse en los siguientes ejemplos

IDEA Y METODOLOGÍA

Para hacer una buena estimación del logaritmo base diez de un número real y no ver la necesidad de utilizar calculadoras científicas o tablas especiales, trabajaremos una fórmula que se dedujo de una serie de poderes de Taylor:

Se muestra una serie de poderes de Taylor para calcular el logaritmo natural de un número "z". A partir de esta fórmula, y aplicando técnicas matemáticas avanzadas fue posible encontrar una expresión más simple para realizar el cálculo de una buena aproximación del logaritmo de la base diez de cualquier número real positivo.

Entrada Relacionada: Cero por infinito

El objetivo es proporcionar un método simple para los estudiosos de las matemáticas a todos los niveles que nos permita hacer una buena estimación en el cálculo de los logaritmos y nos ahorre el uso de calculadoras.