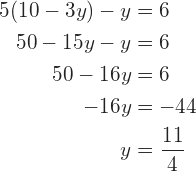Discusión de una ecuación
- Ecuación lineal: es una ecuación polinómica de grado uno, con una o varias incógnitas.
- Ecuaciones equivalentes: cuando tienen la misma solución(es).
Para hacer ecuaciones equivalentes podemos multiplicar o dividir por un número diferente de cero los dos miembros de la ecuación; así obtenemos una ecuación equivalente a la ecuación dada.
- Sistemas de ecuaciones lineales: varias ecuaciones dadas para determinar la solución o soluciones comunes a todas ellas forman un sistema de ecuaciones.
Un sistema de ecuaciones lineales con dos incógnitas representa un conjunto de líneas; su resolución consiste en averiguar si todas ellas tienen un punto común y localizarlo.
- Sistemas de ecuaciones equivalentes: dos sistemas de ecuaciones son equivalentes si tienen las mismas soluciones. Dos sistemas pueden ser equivalentes sin las ecuaciones que lo forman.
Un sistema de ecuaciones puede tener solución, ser compatible, o no tener solución, ser incompatible.
Los sistemas compatibles pueden tener solución; y se llaman compatibles determinados o tienen soluciones infinitas; entonces se llaman compatibles indeterminados
Ejercicio de discusión de una ecuación

Hallamos el rango de la matriz de los coeficientes.


![]()
![]()
Hallamos el rango de la matriz ampliada.


Aplicamos el teorema de Rouché
![]()
![]()
Resolvemos el sistema compatible determinado por la regla de Cramer (tambíén se puede resolver mediante el método de Gauss).


![]()
Contenido