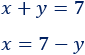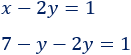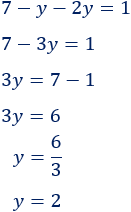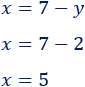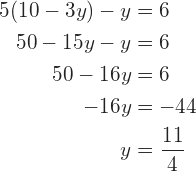
¿Qué es un sistema de ecuaciones?
Un sistema de ecuaciones es un conjunto de dos o más ecuaciones con varias incógnitas en las que queremos encontrar una solución común.
Esta vez resolveremos un sistema de dos ecuaciones lineales con dos incógnitas.
Una ecuación lineal con dos incógnitas es una igualdad del tipo ax+by=c, donde a, b y c son números, y "x" e "y" son las incógnitas.
Una solución es cualquier par de números que cumpla con la ecuación.
Método de Sustitución paso a paso
- Elegimos una de las incógnitas.
- Aclaramos esta incógnita en una de las ecuaciones.
- Reemplazamos las incógnitas en la otra ecuación.
- Resolvemos la ecuación de primer grado.
- Calculamos la otra incógnita sustituyendo la incógnita obtenida.
Ejercicios resueltos de sistemas de ecuaciones por el método de sustitución
Ejemplo:
Despejamos la x en la primera ecuación:
Ahora, sustituimos la expresión algebraica en la segunda, es decir, escribimos 7-y donde aparece x:
Resolvemos la ecuación:
Como ya sabemos y, podemos calcular x a partir de la ecuación que obtuvimos al aclarar x:
Por lo tanto, la solución del sistema es x=5 y y=2
Contenido