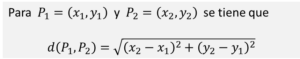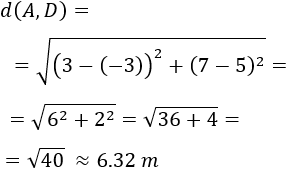
Distancia entre dos puntos
Dadas las coordenadas de dos puntos, P1 y P2, se deduce la fórmula de la distancia entre estos dos puntos. La prueba utiliza el teorema de Pitágoras. Un ejemplo muestra cómo usar la fórmula para determinar la distancia entre dos puntos dadas sus coordenadas. La fórmula de la distancia utiliza las coordenadas de los puntos.
Distancia entre dos puntos ejercicios
Para calcular la distancia entre dos puntos debemos conocer primero las coordenadas de estos puntos. Tomaremos dos puntos cualesquiera y luego, a partir de ellos, generaremos un criterio para cualquier par de puntos para calcular la distancia.
Serán los puntos A=(x,y) y B=(w,z), dos puntos que pertenecen al primer cuadrante del plano cartesiano. Calcula la distancia entre ellos.
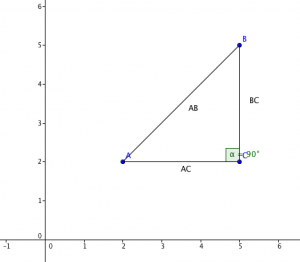
Para generar este cálculo, debemos ubicar los puntos en el plano cartesiano de manera que al generar el segmento que los puntos restan, éste no sea paralelo a ningún eje de coordenadas. Una vez localizados los puntos, debemos localizar un tercer punto de referencia que llamaremos C, que tendrá las coordenadas C=(w,y) para que este punto genere un triángulo rectángulo y sea precisamente el vértice del ángulo recto. Siendo precisamente un gráfico como el que veremos a continuación.
La idea de formar un triángulo rectángulo es que a partir de él se puede utilizar el teorema de Pitágoras para calcular la distancia de la hipotenusa, que es el segmento particular que es de interés. Podemos calcular la distancia de los catetos del triángulo rectángulo para saber la distancia de la hipotenusa que representa la distancia entre el punto A y el punto B.
La distancia de los catetos AC será (w-x) y la del cateto BC será (z-y), por lo tanto, por el teorema de Pitágoras definimos lo siguiente.
Por lo tanto el valor de la distancia AB será:
Ejemplo:
Calcular la distancia entre los puntos R=(5,6) y T=(2,2)
Contenido