Ejercicios de vectores resueltos gráficamente

La adición de vectores es la operación de adición entre vectores que da lugar a otro vector. Los vectores se caracterizan por su magnitud, así como por su dirección y sentido. Por lo tanto, no es posible, en general, sumarlos como se haría con cantidades escalares, es decir, sumar números. El vector que se obtiene de la suma de varios vectores se denomina vector resultante. En la Mecánica hablamos de la fuerza resultante, que es la suma vectorial de todas las fuerzas de un cuerpo. Esta resultante es equivalente al conjunto o sistema de fuerzas. Para especificar completamente la suma vectorial es necesario indicar la magnitud y la unidad, la dirección y el sentido. Es importante señalar que al sumar los vectores, éstos deben representar la misma magnitud física, por lo que la suma vectorial es una operación homogénea. Esto significa que podemos sumar una fuerza con otra, pero no una fuerza con un desplazamiento, ya que el resultado no tiene sentido.

Suma de vectores

La suma de los vectores A y B puede visualizarse gráficamente como dos trayectorias consecutivas, donde la suma de los vectores corresponde a la distancia del vector desde el punto de inicio hasta el punto final. A la izquierda tenemos una representación de los vectores mediante flechas dibujadas a escala. El comienzo del vector B se coloca sobre el final del vector A. La suma vectorial R se dibuja como el vector que va desde el punto inicial del vector A hasta el punto final del vector B.

El proceso anterior puede realizarse matemáticamente encontrando los componentes de A y B, combinándolos para formar los componentes de R, y luego convirtiéndolos a la forma polar.

Entrada Relacionada: Distancia entre dos puntos ejercicios

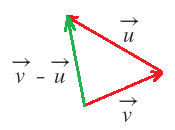
Resta de vectores

La sustracción de vectores es una operación que se realiza con dos de estos segmentos. Para realizar la sustracción de dos vectores, se toma un rector y se le suma su opuesto.

Producto de un vector por un número

Dado un vector u = (x,y) y un número real k, el producto vectorial k.u tiene como componentes el producto de los componentes de u por k.

k.u = k.(x,y) = (k.x , k.y)

Gráficamente

El producto del número k por el vector u es otro vector que:

tiene la misma dirección que u;
tiene la misma dirección que u si k>0, y la dirección opuesta si k<0;
tiene por módulo el producto del módulo de u por el valor absoluto de k: |k|.|u|;

Contenido