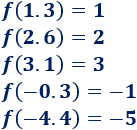
¿Qué es la imagen de una función?
El dominio de una función es el conjunto en el que se define la función.
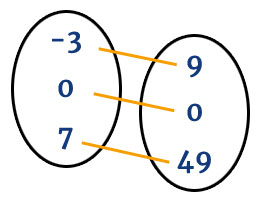
La imagen, trayectoria o rango de una función es el conjunto de imágenes de los elementos de su dominio.
En una función f:A→B, A es el dominio y B es el camino.
Muchas veces, por simplicidad, se proporciona un dominio y un camino genéricos. En este caso, la ruta genérica se llama codominio y este conjunto contiene como subconjunto la ruta de la función.
Casos generales
Cada función tiene un dominio y un camino diferente, pero tenemos algunas reglas generales:
- El dominio y la imagen de una función polinómica es el conjunto de las reales.
- El dominio de un logaritmo es el conjunto de los reales que hacen su argumento positivo.
- El dominio de una función racional es el conjunto de los reales, excepto los números que cancelan el denominador.
- El dominio de una raíz de orden par es el conjunto de los reales que hacen su raíz no negativa. El camino es un subconjunto de los reales no negativos.
Imagen de una función ejercicios resueltos
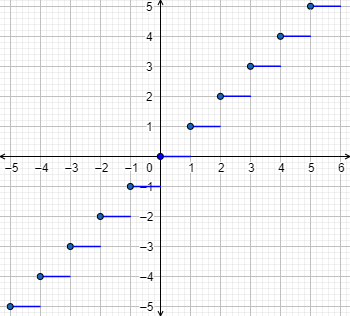
Determinar el dominio y la imagen de la función cuya gráfica es la siguiente:
Calcular las imágenes de 1.3, 2.6, 3.1, -0.3 y -4.4.
El dominio es todos los reales.
La imagen es el conjunto de los números naturales, N.
Se trata de la función parte entera:
Calculamos las imágenes:
Contenido