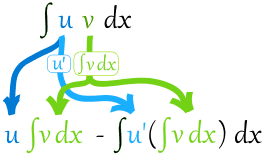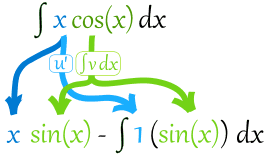Integrate step by step
En el cálculo, y más generalmente en el análisis matemático, la integración por partes o integración parcial es un proceso que encuentra la integral de un producto de funciones en términos de la integral del producto de su derivado y antiderivado. Se utiliza frecuentemente para transformar el antiderivado de un producto de funciones en un antiderivado para el que se puede encontrar más fácilmente una solución. La regla puede pensarse como una versión integral de la regla de diferenciación del producto.
Integrate step by step
∫u v dx = u∫v dx −∫u' (∫v dx) dx
- u es la función u(x)
- v es la función v(x)
- u' es el derivado de la función u(x)
Como un diagrama:
Integrate step by step example
∫x cos(x) dx
Hemos multiplicado x por cos(x), así que la integración por partes es una buena elección.
Primero elige qué funciones para u y v:
u = x
v = cos(x)
Así que ahora está en el formato ∫u v dx podemos proceder:
Diferenciar u: u' = x' = 1
Integrar v: ∫v dx = ∫cos(x) dx = sin(x)
Ahora podemos juntarlo:
Simplificar y resolver:
x sin(x) - ∫sin(x) dx
x sin(x) + cos(x) + C
Contenido