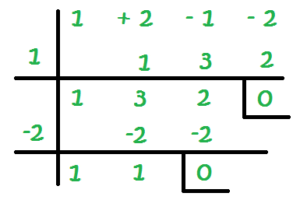
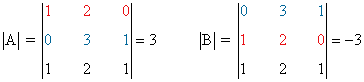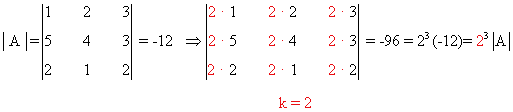Ejercicios de determinantes

El determinante de una matriz de dimensiones mxn es el resultado de restar la multiplicación de los elementos de la diagonal principal con la multiplicación de los elementos de la diagonal secundaria. En otras palabras, el determinante de una matriz de 2×2 se obtiene dibujando una X sobre sus elementos. Primero se dibuja la diagonal que comienza en la parte superior del lado izquierdo de la X (diagonal principal). Luego dibujamos la diagonal que comienza arriba en el lado derecho de la X (diagonal secundaria). Para calcular el determinante de una matriz, necesitamos que su dimensión tenga el mismo número de filas (m) y columnas (n). Por lo tanto, m=n. La dimensión de una matriz se representa como la multiplicación de la dimensión de la fila con la dimensión de la columna. Existen otras formas más complejas de calcular el determinante de una matriz de dimensión mayor que 2×2. Estas formas se conocen como la regla de Laplace y la regla de Sarrus.

Propiedades de los determinantes

El determinante de una matriz y de su traspuesta es el mismo.
| A | = | A^t|

Como consecuencia , toda propiedad que sea válida para filas lo será también para columnas y viceversa. Entonces llamaremos en general líneas a las filas o a las columnas.

El determinante del producto de dos matrices cuadradas A y B es igual al producto de los determinantes de A y de BSi A y B son dos matrices cuadradas del mismo orden.
| A · B | = | A | · | B |
Si multiplicamos a una línea por un número k, el determinante queda multiplicado por dicho número:k · |A|
Si A es una matriz de orden n y k es un número real:
|k · A | = kⁿ|A|
Si se intercambian dos líneas de un determinado, entonces su signo cambia.
Si en un determinado los elementos de una línea son sumas de dos sumandos, puede descomponerse en una suma de dos determinados.
Si una matriz tiene una línea nula su determinante vale cero.
Si una matriz tiene dos líneas proporcionales o iguales su determinante vale cero.
Si una línea puede ser expresada como una combinación lineal de otras líneas su determinante vale cero.
Si a una línea se le añade una combinación lineal de otras líneas paralelas su determinante no cambia. Es decir, si se le añade otra línea multiplicada por un número real, su determinante no cambia.