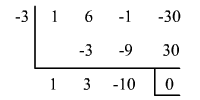
Factorización de polinomios y teorema de factores
Hay dos campos en los que se puede aplicar el teorema del factor para la factorización de polinomios, de manera que se puedan encontrar las raíces de una ecuación de polinomios. Esto se describe como consecuencia directa de que los problemas son esencialmente equivalentes.
El teorema del factor también puede utilizarse para eliminar los ceros conocidos de un polinomio. Dejando intactos todos los ceros desconocidos, produce un polinomio menor cuyos grados ceros son más fáciles de encontrar en la ecuación. El método para factorizar los ceros sería el siguiente a través del teorema
Adivinar un cero a del polinomio f. Esto suele ser muy difícil de hacer, ya que los problemas en los libros de ecuaciones y problemas matemáticos, que implican la resolución de una ecuación de naturaleza matemática, a menudo no se centran en la enseñanza de algunas raíces fáciles de descubrir. Por lo tanto, se recomienda seguir una educación más avanzada para que cuando se aplique el teorema del factor, sea más fácil de hacer.
- Utilice el teorema para concluir que (x - a) es un factor que pertenece a f(x)
- Calcula el polinomio g(x) f(x) / (x-a). Esto puede verse en un ejemplo en el que se utiliza la división larga del polinomio o la división sintética.
- Al final, se puede concluir que cualquier raíz donde x es diferente, perteneciente a f(z)= 0 es una raíz de g(x). Mirándola desde el grado polinómico de g, es uno menos que el de f, siendo "más simple" en cuestión encontrar los ceros restantes. Esto, por supuesto, si se estudia g correctamente.
Explicación del teorema del factor
Como se señala en el caso del teorema del resto, si un polinomio que es p(x) se divide por un factor x-a de ese polinomio, lo que se obtendrá es un resto cero. La expresión del algoritmo para dividir el polinomio sería la siguiente:
P (x) = ( x - a) q (x) + r (x)
Donde si x - a es de hecho un factor de p (x), entonces el resto después de la división por x - a será cero. Es decir: p (x) = ( x - a). En términos del teorema del resto, esto significa que x - a es un factor de p (x), así que el resto, cuando hagamos la división sintética por x=a, será cero.
El punto de todo lo anterior es que el teorema del factor es el inverso del teorema del resto. Si dividimos sintéticamente un polinomio x = a y obtenemos un resto cero, entonces no sólo es x = un cero del polinomio. Esto se conoce gracias al teorema del residuo. Pero x - a es también un factor del polinomio, que se obtiene gracias al teorema del factor. Como se puede ver, ambos teoremas son bastante similares, en los que uno es el reverso del otro y se puede ver fácilmente en la práctica.
El punto principal del teorema de factores es no hacer la división larga de un polinomio dado por un factor dado. Al igual que con el resto de teoremas que tienen la misma función. Este teorema en sí mismo no busca repetir lo que ya sabe, sino que trata de simplificar la vida de las personas. Una ventaja que muy pocos conocen. En el caso de que estés tratando de resolver un ejercicio del teorema del factor, debes aplicar la división sintética y luego comprobar si hay un resto cero.