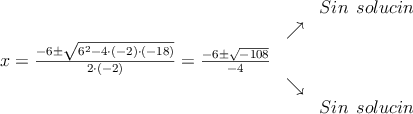Ecuaciones de segundo grado con paréntesis
Sabemos que una ecuación es una relación matemática entre números y letras. Normalmente trabajamos con ecuaciones en las que sólo hay una letra, llamada incognita, que suele ser x. La resolución de la ecuación consiste en encontrar un valor (o varios) que, al sustituirlo por la incognita, hace que la igualdad sea verdadera.
Ecuación de segundo grado con paréntesis
- Resuelve la ecuación
Para resolver ecuaciones de segundo grado podemos aplicar la Fórmula general, pero antes debemos ordenar la ecuación hasta que quede de la forma .También debemos recordar que signo menos delante de paréntesis, le cambia el signo a todos los términos del paréntesis
Ahora pasamos todo a la izquierda del signo igual
Ahora unificamos términos (juntamos las x² con las x², las x con las x y los números con los números)
Por ejemplo: en x² tenemos -3x²+x²=-2x²
Finalmente quedaría así:
Ahora ya podemos aplicar la fórmula