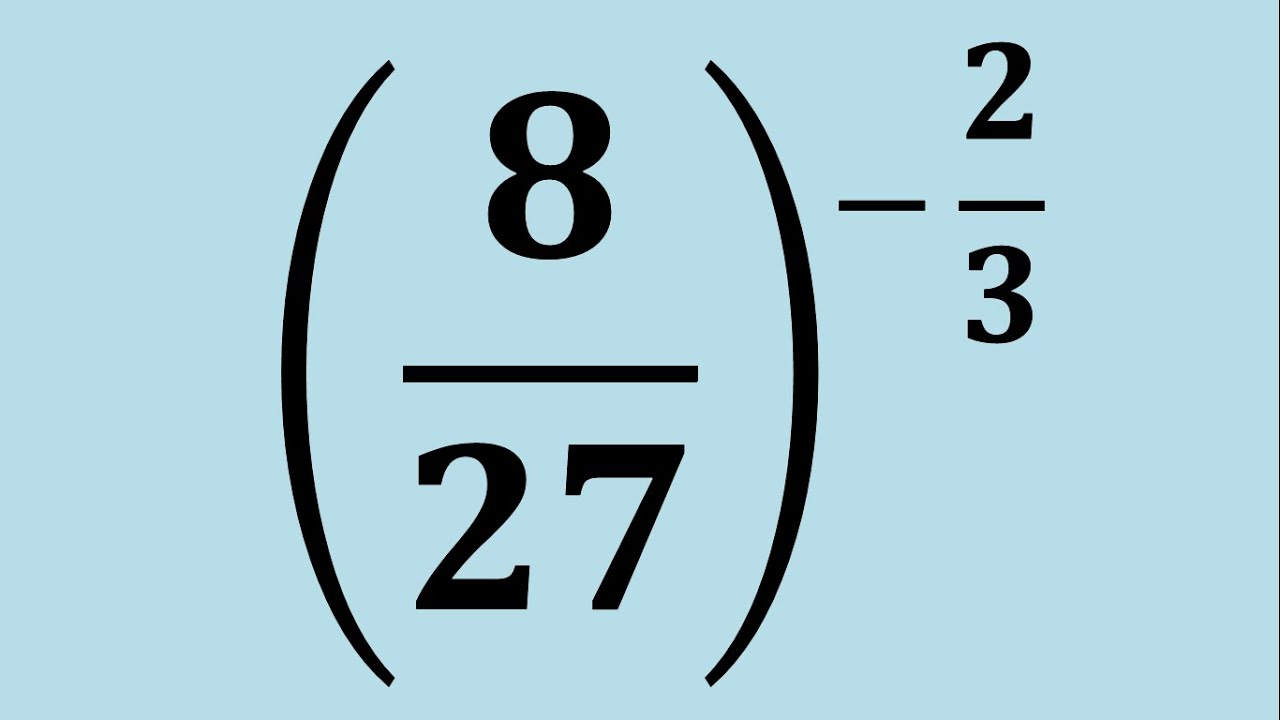
Exponente fraccionario
Es muy conveniente para el propósito de calcular con las raíces, transformándolas en potencias exponenciales fraccionarias:
(Esta última forma se deduce aplicando las propiedades de los poderes, en particular, el poder de un poder:
Con esta técnica, podemos deducir las reglas del cálculo con raíces de las reglas del cálculo con potencias, convirtiendo previamente los radicales en potencias de exponente fraccionario.
Potencias con exponente fraccionario. Cómo resolver un número elevado a una fracción
Llamamos la raíz n-ésima de un número dado a al número b que elevado a n nos da a.
Un radical es equivalente a un exponente fraccionario de potencia en el que el denominador de la fracción es el índice del radical y el numerador de la fracción es el exponente del radicando.
Operaciones con potencias de exponente fraccionario
Las potencias de exponente fraccionario verifican las mismas propiedades que las potencias de exponente entero. Repasémoslas una a una:
Producto de potencias de la misma base
El producto de dos potencias de la misma base es otra potencia de la misma base cuyo exponente es la suma de los exponentes de los factores
am * an = am+n
La regla anterior es verdadera cualquiera que sea la base y los exponentes m y n, sean positivos o negativos, enteros o fraccionarios.
Contenido