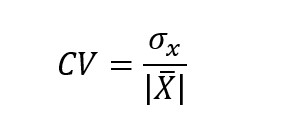
Ejercicios de medidas de dispersión

Las medidas de dispersión son números que indican si una variable se mueve mucho, poco, más o menos que otra. El motivo de este tipo de medida es conocer de forma resumida una característica de la variable estudiada. En este sentido, deben acompañar a las medidas de tendencia central. Juntas, proporcionan información de un vistazo que podemos utilizar para comparar y, si es necesario, tomar decisiones.

Principales medidas de dispersión

La dispersión o variación es una característica importante de un conjunto de datos porque trata de dar una idea de cuán difundidos están los datos. Existen varias medidas de dispersión, algunas de las cuales son el Rango, la Desviación Media, la Varianza y la Desviación Estándar.

Rango

Indica la dispersión entre los valores extremos de una variable. se calcula como la diferencia entre el valor más alto y el más bajo de la variable. Se denota como R.

Para los datos ordenados se calcula como:

R = x(n) - x(1)

Donde: x(n): es el valor más alto de la variable. x(n): es el valor más bajo de la variable.

Desviación media

Es la media aritmética de los valores absolutos de las diferencias de cada dato con respecto a la media.

Desviación estándar

La desviación estándar mide el grado de disección de los datos respecto de la media, se denota como s para una muestra o como σ para la población.

Variación

Es otro parámetro que se utiliza para medir la dispersión de los valores de una variable con respecto al promedio. Corresponde a la media aritmética de los cuadrados de las desviaciones de la media.

Entrada Relacionada: Regla de 3 compuesta

Coeficiente de variación

Permite determinar la relación entre la desviación estándar (s) y la media. Se llama CV. El coeficiente de variación permite decidir más claramente la dispersión de los datos.

Ejemplos de medidas de dispersión

Supongamos que las edades de un grupo de jóvenes son las siguientes: 18, 20, 34, 26, 17, 14, 30.

Calcula la desviación media de los datos.

Primero se calcula la media o media aritmética de los datos, sumándolos y dividiendo el resultado por el número de datos.

Luego se calcula la diferencia de cada dato con el promedio en valor absoluto y luego se suman las diferencias, es decir, en valor absoluto significa que siempre será positivo, después se divide el resultado por el número de datos.