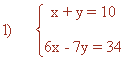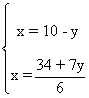Problemas de sistemas de ecuaciones con dos incognitas

Un sistema lineal de ecuaciones, o sistema de ecuaciones lineales o incluso, para ser breve, sistema de ecuaciones, es un conjunto de ecuaciones de primer grado con varias incógnitas. La solución de un sistema lineal de ecuaciones es un conjunto de números que, sustituyendo cada una de las incógnitas, convierte todas las ecuaciones en equivalentes numéricos correctos.

Sistema de ecuaciones

Comencemos directamente definiendo que un sistema de ecuaciones es un conjunto de dos o más ecuaciones que contienen dos o más incógnitas, estas ecuaciones están relacionadas entre sí ya que el valor de las incógnitas satisface todas las ecuaciones al mismo tiempo.

En esta ocasión estudiaremos los sistemas de ecuaciones 2x2 (2 ecuaciones y 2 incógnitas). Este tipo de sistemas es muy común en las tareas escolares, en las pruebas de admisión y son tan versátiles que pueden ser utilizados sin ningún problema para representar casos reales. Hay muchas maneras de resolver un problema de este tipo, algunas un poco más difíciles y complicadas que otras, pero en esta página nos centraremos en dos formas diferentes que se ven a lo largo de la escuela secundaria, es decir: la forma algebraica y la forma gráfica.

La primera se desglosa en varios procedimientos algebraicos diferentes: El método de reducción (también conocido como suma y resta), el método de sustitución y el método de ecualización; y por otro lado el método gráfico consiste en interpretar y analizar de forma gráfica el comportamiento de ambas ecuaciones en el mismo plano cartesiano.

Método de suma y resta

El método de suma y resta, también conocido como reducción, es un método en el que el objetivo es eliminar una de las dos incógnitas utilizando una suma algebraica. Esta eliminación puede ocurrir de dos maneras:

Entrada Relacionada: Monotonía de una función

La forma directa es cuando nos damos cuenta de que en ambas ecuaciones del sistema, la misma incógnita tiene el mismo coeficiente sólo que con signo opuesto, como se puede ver en la imagen (haga clic para ver la imagen a pantalla completa). En este caso, el primer paso es colocar ambas ecuaciones una encima de la otra de manera que cada tipo de desconocido forme una columna, así como la parte sin el desconocido (que siempre debe estar a la derecha del igual).

Después sumamos como hemos aprendido en los apartados anteriores y nos damos cuenta de que una incógnita se elimina porque su coeficiente se convierte en cero como en el ejemplo. Luego resolvemos la ecuación de primer grado que hemos creado para obtener el valor del primer literal.

Como paso final sustituimos este valor en una de las ecuaciones originales, para ello donde está la letra, utilizamos paréntesis y colocamos su valor dentro de ellos, realizamos las operaciones correspondientes para resolver esta segunda ecuación de primer grado y así obtendremos el segundo literal.

Esto resolvería nuestro sistema de ecuaciones donde la respuesta sería el valor de ambos literales al mismo tiempo.

Detección de múltiplos: Esta forma procede cuando existe una relación entre cualquiera de las dos letras de ambas ecuaciones en cuanto a si estamos hablando de múltiplos de sus coeficientes. Un ejemplo sería que una ecuación es 2x+4y=20 y la otra es 3x+8y=43 donde la desconocida y en ambos casos tiene coeficientes múltiplos de 4.

En este método no importa si los coeficientes son de signos opuestos, sólo que son múltiplos.

Entrada Relacionada: Representar gráficamente

El procedimiento se inicia de la siguiente manera (se puede ver con números en la imagen de la izquierda).

Algo muy importante de este método es que su finalidad es lograr eliminar una de las incógnitas de ambas ecuaciones para encontrar la que no ha sido eliminada. De esta manera y cuando obtenemos la segunda desconocida podemos usar ese resultado para encontrar la primera que hemos eliminado. Por eso en este método se suma algebraicamente para lograr ese propósito.

Método de igualación

Este método suele ser sencillo para aquellos que lo encuentran fácil de despejar.

El método se llama así porque, para resolver el sistema de ecuaciones debemos aclarar la misma letra en ambas ecuaciones, esto es para igualar el lado derecho de la igualdad y resolver una ecuación de primer grado con la misma desconocida en ambos lados.

En la imagen de la izquierda podemos ver el mismo sistema de ecuaciones que se resolvió anteriormente, la diferencia con el método de sustitución anterior es que aquí la X se despeja para ambas ecuaciones, de esta manera las partes derechas de los despejes se ecualizan para finalmente encontrar el valor de la y.

Encontrando el valor de y podemos sustituirlo en cualquiera de los 2 claros de x para encontrar el valor de esta misma letra, para este caso (como en los anteriores) el resultado es y=10 y x=35.