¿Qué es el Teorema del Valor Medio?
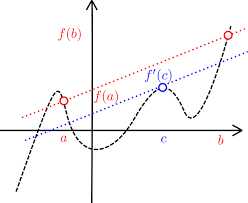
Cuando hablamos de matemáticas, el Teorema del Valor Medio establece una afirmación que dice: "para un arco plano dado entre dos puntos finales, hay al menos un punto donde la tangente al arco es paralela a la secante a través de sus puntos finales". El teorema se utiliza para probar afirmaciones sobre una función que se encuentra en un intervalo a partir de hipótesis locales sobre las derivadas en los puntos del intervalo.
Esto se observa mejor, cuando F es una función continua en el intervalo cerrado, que siendo [a,b] y distinguible en el intervalo cerrado (a,b), entonces hay un punto en C donde es paralela a la función. Este teorema es uno de los más utilizados en matemáticas y álgebra, siendo utilizado para obtener un análisis real.
La primera vez que se sabe que se utilizó el teorema del valor medio fue en el año 1900, en el sentido definido. Siendo más específico en el sentido1. Por lo que parece, el teorema está realmente en la prueba del teorema fundamental de cálculo. Ya que se basa en sí mismo en última instancia en las propiedades de los números reales. De hecho, existe una ligera generalización conocida como el teorema del valor medio de Cauchy, que se utiliza para la generalización a derivados superiores.
Aplicación del teorema del valor medio
El teorema puede aplicarse fácilmente en ejemplos de la vida real como los siguientes:
Usando el tiempo que le tomó viajar una milla, puede calcular la velocidad promedio que tomó en el viaje. Sabiendo que la velocidad media = distancia total / tiempo total, entonces la velocidad media puede ser calculada haciendo:
Velocidad media = (1 milla / 52,91 segundos) x (3600 segundos / 1 hora) = 68,04 mph
El valor original se dio en millas por segundo, por lo que tuvo que ser multiplicado por 3600 / 1 hora para obtenerlo en millas originales.
Ejemplos del teorema en la vida real
Un camionero viaja 163 millas en una carretera de peaje con un límite de velocidad de 70 millas por hora. El camionero completa el viaje de 163 millas en 2 horas. Al final de la carretera de peaje, el camionero recibe una multa por exceso de velocidad. ¿Por qué sucede esto?
Bueno, para resolver este problema puedes usar el término medio. Como la posición del camión es continua en el intervalo cerrado, distinguible en el intervalo abierto, no hubo discontinuidad en el gráfico de posición. Que es el camión que pasó por cada punto de la carretera de la cabina de peaje a la otra cabina de peaje.
No hay agujeros de gusano o agujeros negros. También hay un pico en el gráfico de posición que no sería divertido viajar a 70 millas por hora. Aplicando el término de valor promedio, se establece que en un punto la velocidad promedio del usuario de la carretera. Eso debería ser igual a la velocidad instantánea del camión. El resultado se vería así:
Velocidad media = distancia total (viaje) / tiempo total
163 millas / 2 horas = 81.5 mph
Entonces, al menos una vez en el tiempo en la carretera de peaje, el camionero iba a 81,5 millas por hora, muy por encima del límite de velocidad. Así es como se puede aplicar el valor promedio para que un camionero reciba un boleto.
¿Qué significa esta aplicación?
Como cualquier error, es posible que haya un error en el experimento. Pero las fuentes de estos errores podrían ser un error humano en el tiempo, marcadores de millas que no están colocados exactamente a una milla de distancia o la aguja del velocímetro que no se ajusta exactamente a 70 mph. Pero, con los datos dados, no hay duda de que uno puede decir cuál fue la velocidad promedio.
Además, el valor promedio puede ser usado para probar la precisión del velocímetro. Ajustando el control de crucero del coche a 70 mph, y calculando el tiempo que tarda en recorrer una milla. Luego, esta información podría usarse para probar la precisión del velocímetro y averiguar si hay un error.
Contenido