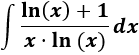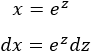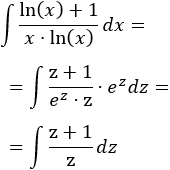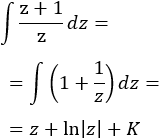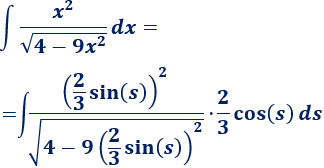
Integrales por sustitución

Como su nombre lo indica, este método de integración consiste en la aplicación de un cambio de variable para simplificar el integrando.

Integrales por sustitución

El método de integración por sustitución o por cambio de la variable se basa en hacer una sustitución adecuada de la variable que permita convertir la integración en algo sencillo con una simple integral o antideriva. En muchos casos, cuando las integrales no son triviales, se puede tomar una integral de tabla para encontrar fácilmente su primitiva. Este método realiza lo contrario de la regla de la cadena en la derivación.

Elija una función de cambio variable z de x
Despeja x para calcular dx
Sustituir en la integral, resolverla y deshacer el cambio de variable

La dificultad del método consiste en elegir un cambio útil, ya que, de lo contrario, la integral resultante puede ser de mayor dificultad. En el siguiente cuadro se recogen los cambios variables que tienen una alta probabilidad de funcionar en las integrales que habitualmente veremos:

El método de cambio de variable es un poco más complicado cuando se aplica en integrales definidas porque al cambiar la variable, los extremos de la integración deben ser actualizados. Por ejemplo, si los extremos de la integral inicial con la variable x son 0 y 1 y la nueva variable es z=2x, entonces los nuevos extremos serán 0 y 2. Una forma de evitar este problema es resolver primero la integral indefinida.