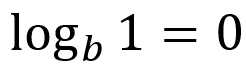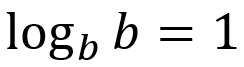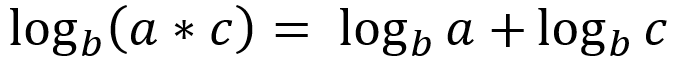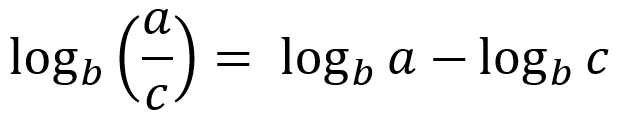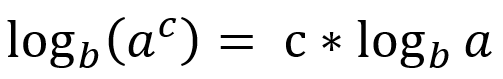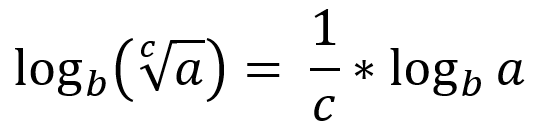Propiedades de los logaritmos
A primera vista, los logaritmos siempre parecen dificultar las cosas. Por lo tanto, es crucial conocer muy bien las propiedades de ellos. Como verán a continuación, las expresiones pueden ser transformadas.
El logaritmo de la unidad: Si recordamos la propiedad de las potencias llamadas "producto del exponente cero", podemos afirmar que para cualquier base, el logaritmo -tanto neperiano como común- de 1, es siempre 0.
Logaritmo de la base: El logaritmo del argumento cuando coincide con la base, es 1.
Logaritmo de un producto: Cuando tenemos dos números multiplicándose entre sí, su logaritmo es igual a la suma de ambos logaritmos (siempre en la misma base).
Del mismo modo, y como vimos con los poderes fácticos, es importante tener en cuenta la reciprocidad. Tanto con los últimos como con los siguientes. Es decir, a veces es conveniente separar un producto en una suma de logaritmos, pero otras veces, será útil unir una suma de logaritmos en un solo producto. Recuerde que es necesario que ambos tengan la misma base.
Logaritmo de una división: Por otro lado, el logaritmo de una división puede ser separado en una resta de logaritmos de la misma base.
Logaritmo de una potencia: El exponente del argumento, luego pasará multiplicándose al logaritmo del argumento.
De nuevo, recuerde que el camino inverso es importante. Pasar de una multiplicación escalar-logarítmica, al logaritmo de una exponencial, es ampliamente utilizado en matemáticas.
Logaritmo de una raíz: De la misma manera, si el argumento tiene su raíz en una raíz, el índice será el que pase multiplicando al logaritmo del argumento, pero esta vez como denominador de una fracción cuyo nombre es 1.
Cambio de base del logaritmo: Cuando buscamos el logaritmo y no sabemos cómo calcularlo, esta propiedad es esencial. Ya que nos permite cambiar la base a cualquier expresión logarítmica. Lo que debemos hacer es formar una fracción donde el numerador es el logaritmo en cualquier base del argumento original; y el denominador es el logaritmo, en la misma base del numerador, pero esta vez el argumento será la base original. Formando lo siguiente: