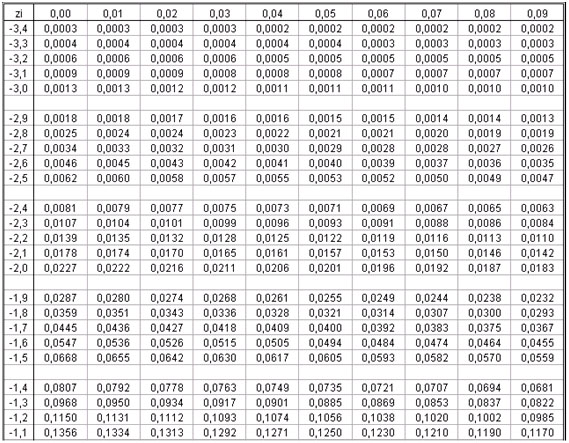
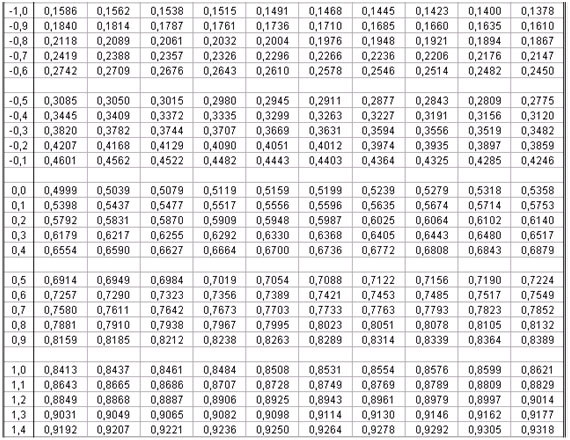
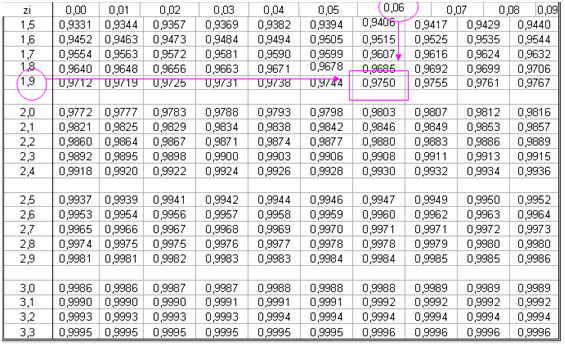
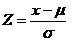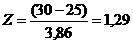Tabla de distribución normal estándar valores negativos

Se dice que muchos fenómenos en el campo de la salud se distribuyen normalmente. Esto significa que si uno toma al azar un número suficientemente grande de casos y construye un polígono de frecuencia con alguna variable continua, por ejemplo, peso, altura, presión sanguínea o temperatura, se obtendrá una curva de características particulares, llamada distribución normal. Es la base del análisis estadístico, ya que casi todas las inferencias estadísticas se basan en ella.

El gráfico de la distribución normal tiene la forma de una campana, por lo que también se conoce como la campana de Gauss. Sus características son las siguientes:

- Es una distribución simétrica.
- Es asintótica, es decir, sus extremos nunca tocan el eje horizontal, cuyos valores tienden a ser infinitos.
- En el centro de la curva están la media, la mediana y la moda.
- El área total bajo la curva representa el 100% de los casos.
- Los elementos centrales del modelo son la media y la varianza.

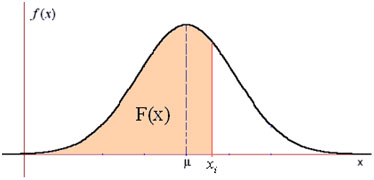
Esta distribución es un modelo matemático que permite determinar las probabilidades de ocurrencia para diferentes valores de la variable. Así, para determinar la probabilidad de encontrar un valor de la variable que sea igual o menor que un determinado valor xi, conociendo la media y la varianza de un conjunto de datos, estos valores (media, varianza y xi) deben ser sustituidos en la fórmula matemática del modelo. El cálculo es bastante complejo pero, afortunadamente, existen tablas estandarizadas que permiten evitar este procedimiento.

En el gráfico, la zona sombreada corresponde a la probabilidad de encontrar un valor de la variable que sea igual o inferior a un valor dado. Esa probabilidad es la que aprenderemos a determinar utilizando una tabla estandarizada.

Tabla de la distribución normal

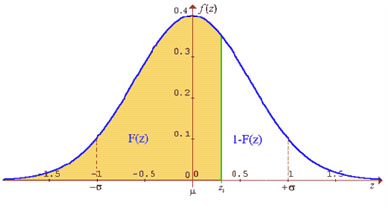
La tabla de distribución normal presenta los valores de probabilidad de una variable estándar Z, con una media igual a 0 y una varianza igual a 1.

Para utilizar la tabla, debemos siempre estandarizar la variable por medio de la expresión:

Siendo el valor del interés; la media de nuestra variable y su desviación estándar. Recuerde que y corresponden a parámetros, o valores en el universo, que generalmente no se conocen, por lo que debemos calcular Z usando los datos de nuestra muestra.

En general, el valor de Z se interpreta como el número de desviaciones estándar que se encuentran entre la media y un cierto valor de la variable x. En otras palabras, se puede decir que es la diferencia entre un valor de la variable y la media, expresada como esta diferencia en número de desviaciones estándar.

Suena abstracto, pero con un ejemplo se puede entender mejor:

Supongamos un conjunto de personas con una edad media de 25 años y una desviación estándar de 3,86. Nuestro valor de interés (x) es de 30 años. El valor correspondiente de Z será:

Este valor Z nos dice que la edad de 30 años está 1,29 desviaciones estándar por encima de la media.

Ahora, la tabla de distribución normal da valores de probabilidad para los diferentes valores Z.

¿Cómo se usa la tabla de Z?

Tabla de distribución normal