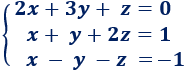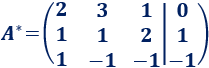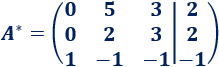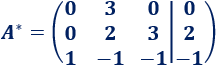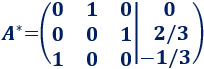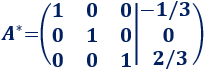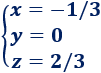Gauss jordan online matrix
Un sistema de ecuaciones lineales puede ser; Compatible determinado: tiene una sola solución. Indeterminado compatible: tiene infinitas soluciones. Incompatible: no tiene solución.
Forma matricial de un sistema
La forma matricial de un sistema de ecuaciones lineales es
donde
- A es la matriz que en la fila k contiene los coeficientes de las incógnitas de la ecuación k.
- X es la matriz columna con las incógnitas.
- B es la matriz columna con los términos independientes de las ecuaciones.
- A∗ es la matriz ampliada o aumentada del sistema, formada por las matrices A y B:
Gauss jordan online matrix ejemplo
La matriz ampliada del sistema es
A fila 1 le restamos dos veces la fila 3 y a la fila 2 le restamos la fila 3:
A la fila 1 le restamos la fila 2:
Dividimos la fila 1 entre 3:
A la fila 3 le sumamos la fila 1 y a la fila 2 le restamos dos veces la fila 1:
Dividimos la fila 2 entre 3:
A la fila 3 le sumamos la fila 2:
Reordenamos las 3 filas:
Ya tenemos resuelto el sistema porque la matriz obtenida es la solución:
El sistema es compatible determinado.
Contenido