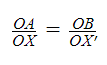
Qué es la razón de dos segmentos
Llamamos proporcionalidad del segmento a la aplicación existente entre el conjunto de cantidades de longitud en sí mismo, de manera que la aplicación es biectiva, conserva el orden, el mismo y también mantiene la correspondencia con la operación de la suma.
Proporcionalidad entre pares de segmentos
Dadas dos líneas r y s que se cortan en el punto O y dadas dos longitudes a y b en cada una de las líneas respectivamente para que determinen los segmentos OA=a y OB=b, como podemos ver en la imagen. Dibujando la línea que conecta los puntos A y B y trazando una línea paralela a ella que corta las líneas r y s en el punto X y X' respectivamente, entonces el segmento OX se hace corresponder con el segmento OX'.
Por lo tanto, se cumple la siguiente relación de proporcionalidad:

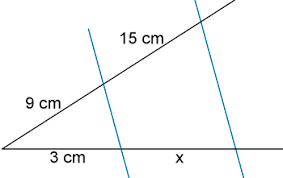
El teorema de Tales
El Teorema de Tales se divide, a la vez, en dos teoremas. El primero de ellos sirve para construir un triángulo como uno ya existente. Estos triángulos tienen ángulos iguales, lo que resulta en que sus lados son homólogos. Es decir, lo que hace es aumentar o disminuir la longitud de sus lados para mantener la misma proporción.
Tales de Mileto explicó este teorema de la siguiente manera:
Si en un triángulo se dibuja una línea paralela a cualquiera de sus lados, se obtiene un triángulo similar al triángulo dado.
El segundo teorema revela una propiedad esencial de los circuncentros de todos los triángulos rectos, estando éstos en el punto medio de su hipotenusa. A su vez, esta construcción geométrica se utiliza ampliamente para imponer condiciones para la construcción de ángulos rectos.
Este teorema se explica de la siguiente manera:
Dejemos que B sea un punto en la circunferencia del diámetro AC y el centro "O", diferente de A y C. Entonces el triángulo ABC, es un triángulo recto donde <ABC = 90º.
¿Para qué sirve el teorema de Tales?
El teorema de Tales se usa principalmente para conocer medidas y proporciones desconocidas.
Su uso principal es en la relación de triángulos, lo que nos permite saber y conocer las proporciones de las medidas de estos triángulos.
El teorema de Tales se utiliza mucho en las construcciones y arquitecturas, nos permiten relacionar medidas, relacionar cargas.
En la ingeniería mecánica es fundamental para los diseños mecánicos, pues este nos permite relacionar diferentes medidas, realizar cálculos y obtener las proporciones necesarias.
Todo lo que se realice bajo conceptos geométricos se le puede aplicar el Teorema de Tales.
Cómo dividir un segmento en partes iguales con el teorema de Tales
Dividamos el segmento AB en tres segmentos iguales.
- Primero dibujamos una línea recta con origen en A que forma con el segmento AB un ángulo de menos de 180º.
- Luego elegimos un segmento U arbitrario y lo llevamos sobre el rayo tres veces. Llamamos P al punto que corresponde a la última división. Luego unimos el punto P con el punto B.
- Finalmente dibujamos paralelo a PB por los puntos de división M y N, obteniendo así los puntos M' y N', que dividen el segmento AB en tres partes iguales.