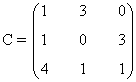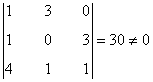Cómo sacar el rango de una matriz

El rango de un arreglo es el número de líneas que son linealmente independientes del arreglo. Una fila es linealmente independiente de las demás cuando no puede establecerse a partir de una combinación lineal de las demás. Si, por el contrario, podemos encontrar una fila a partir de una combinación lineal de las otras, entonces diremos que esa fila es linealmente dependiente. En ese caso esa fila debe ser descartada para el cálculo del rango de la matriz.

¿Cuál es el alcance de una matriz?

El rango de una matriz es el número de filas o columnas que son linealmente independientes.

¿Qué significa que son linealmente independientes?

Linealmente independiente significa que ninguna de ellas, las filas o columnas, pueden combinarse linealmente entre sí.

La dependencia o independencia lineal de un conjunto se observa principalmente entre sus filas, aunque también es posible observarla entre sus columnas.

Por ejemplo, cabe mencionar que el rango de un conjunto de 3×6 es, como máximo, 3. Es decir, el rango de un conjunto de m x n es, como máximo, el menor de los números "m" o "n".

Para calcular el rango de una matriz podemos hacer diferentes métodos, ya sea por determinantes o por el método gaussiano (recomendamos revisar esta entrada previamente).

Las transformaciones que aplicamos a un conjunto por este método no cambian su rango, conservando la dependencia e independencia lineal de las filas transformadas. De esta manera, hacer ceros hasta obtener un conjunto escalonado nos dará la información necesaria.

Así, el rango del conjunto resultante será el número de filas diferentes de ( 0 0 0 ..0).

Entrada Relacionada: Potencia de un punto

Ejemplo de Cómo sacar el rango de una matriz

Encontrar el rango de la matriz C

Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )

Como la matriz es de orden 3, tenemos que rg(C) ≤ 3.

así que encontramos un menor de orden 3, que era el máximo posible. Por lo tanto rg(C) = 3.

Para las matrices cuadradas es un buen método para empezar a calcular el determinante de la propia matriz, porque en caso de que no sea cero, obtenemos que el rango es el orden de la propia matriz.

El rango de la matriz es el orden de la más pequeña no nula.

Contenido