Leyes de kirchhoff ejercicios resueltos

La resolución de los circuitos eléctricos juega un papel muy importante dentro de la electrónica y otras áreas de la física que se relacionan con cuestiones eléctricas. Sin embargo, hay temas a los que deberíamos dedicar más dedicación y atención porque se centran en interesantes principios matemáticos para mejorar nuestra capacidad de resolver problemas. Posiblemente para llegar a las Leyes de Kirchhoff ya has aprendido a reducir las resistencias en serie, o en paralelo y a calcular las corrientes y los voltajes en cada componente, bueno ahora es el momento de aprender algo nuevo

Conceptos previos de las leyes de Kirchhoff

Las leyes de Kirchhoff son dos valores basados en la conservación de la energía y la carga en los circuitos eléctricos. Estos iguales son los dados por la ley de los nodos (corrientes) y la ley de las mallas (voltajes), pero primero, para entender perfectamente las leyes de Kirchhoff, hay que tener en cuenta algunos conceptos previos:

Nodo: Es un punto en común a 2 o más elementos. También mencionamos como nodo algún punto del circuito que queremos destacar. Por ejemplo, para marcar un potencial.
Nodo o unión: Es un punto en común a 3 o más elementos.
Rama: Es cualquier conexión en serie de uno o más elementos entre dos puntos.
Lazo: Es cualquier camino cerrado del circuito.
Malla: Es un bucle que no puede ser dividido y no contiene otro bucle. Según la definición, cada malla es un bucle pero no al revés. También es cierto que una rama no puede ser común a más de dos mallas. En la práctica, todos los bucles suelen llamarse mallas, aunque no lo sean estrictamente.

Entrada Relacionada: Derivadas logarítmicas ejercicios resueltos paso a paso

Primera ley de Kirchhoff. Ley de las corrientes de Kirchhoff

Esta ley también se llama la ley de las corrientes y nos dice que:

En cualquier nodo, la suma de la corriente que entra en ese nodo es igual a la suma de la corriente que sale de él. De la misma manera, la suma algebraica de todas las corrientes que pasan por el nodo es igual a cero.
primera ley de kirchhoff

I1 + I3 = I4 + I2

I1 - I2 + I3 - I4 = 0

Segunda ley de Kirchhoff. Ley de las tensiones de Kirchhoff

Esta ley también se llama la ley de las tensiones y nos dice que

En cada malla la suma de todas las caídas de tensión es igual al total de la tensión suministrada. Igualmente, en cada malla la suma algebraica de las diferencias de potencial eléctrico es igual a cero.

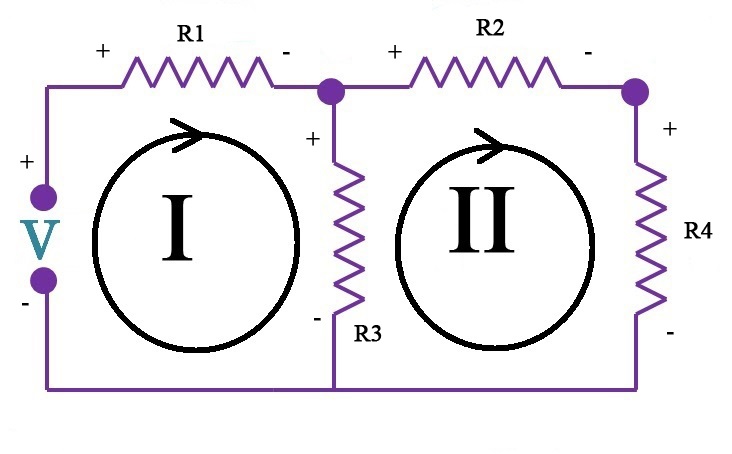
En la malla I:

VR1 + VR3 - V = 0

En la malla II:

VR2 + VR4 - VR3 = 0

Como VR = IR × R, puede ser sustituido en las ecuaciones anteriores si no se tienen los datos de los voltajes de las resistencias. Utilizando la ley de nodos y la ley de malla, se pueden calcular todas las variables que faltan.

Procedimiento para resolver circuitos con las leyes de Kirchhoff

Método de voltaje de nodo

A continuación, explicaré cómo resolver los circuitos eléctricos usando el método del nodo esencial. Para aplicar este método, debemos seguir los siguientes pasos:

Marcamos los nodos esenciales del circuito.
Seleccionamos uno de estos nodos como nodo de referencia (tierra, 0 voltios).
Definir las tensiones de los nodos en el circuito. La tensión de nodo se define como un incremento de tensión desde el nodo de referencia hasta cualquier nodo.
Dibujamos corrientes que salen de cada nodo para cada una de las ramas que convergen en él.
Escribimos el valor de cada una de las corrientes aplicando la siguiente ecuación

Entrada Relacionada: Raíces de polinomios

I = (Vnodo de salida - Vnodo de llegada ±Fuentes cruzadas) / Σ R de la rama

"Cuando tenemos fuentes de tensión en una rama, ponemos el signo + delante si salimos por el terminal + y - si salimos por el terminal -"

Aplicamos la primera ley de Kirchhoff a cada nodo.

Ejercicio resuelto sobre las leyes de Kirchhoff

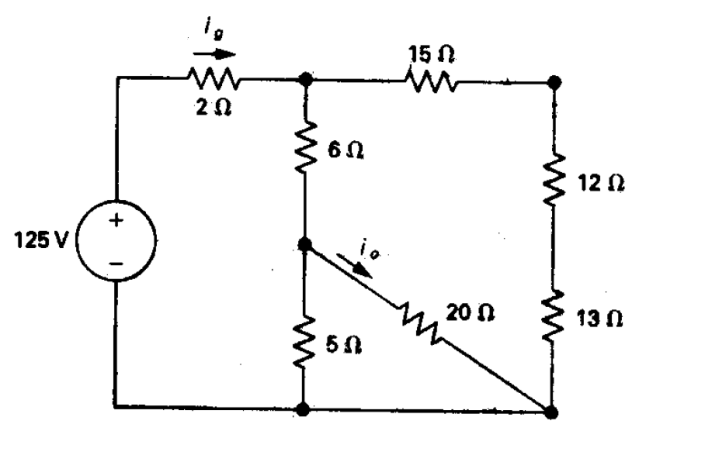
Determinar i0 e ig en el circuito de la figura:

Resolver por el método de voltaje de nodo.
Resolver por el método de la corriente de malla.
Resolver el circuito resultante si eliminamos la resistencia de 2Ω.

Resolviendo por el método del voltaje del nodo

Marcamos los nodos esenciales del circuito.
Seleccionamos uno de estos nodos como nodo de referencia (tierra, 0 voltios).
Definimos las tensiones de los nodos en el circuito. La tensión de nodo se define como un incremento de tensión desde el nodo de referencia hasta cualquier nodo.
Dibujamos corrientes que salen de cada nodo para cada una de las ramas que convergen en él.