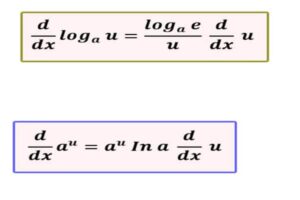Pasos para resolver una ecuación de primer grado
- Si hay denominadores, los reducimos a un denominador común (calculando el m.c.m ) y suprimimos los denominadores.
- Eliminamos los paréntesis aplicando la regla de los signos. Al final tendremos a ambos lados del igual, sólo sumas y restas, algunos términos tendrán x y otros no.
- Transposición de términos: Pasamos todos los términos con x a un lado de la ecuación, los números al otro lado.
- Agrupamos los términos similares y al final despejamos la x obteniendo la solución.
- Comprobamos la solución sustituyendo el valor de la x obtenida en la ecuación. Esto debería darnos el mismo resultado en ambos lados de la ecuación.
Ecuaciones de primer grado
Transposición de términos, cualquiera de los términos que se sumen en un miembro de la ecuación pasa al otro miembro por substracción y viceversa. Cualquiera de los términos que estés multiplicando en un miembro de la ecuación pasa al otro miembro por división y viceversa.
Paso 1: quitamos los paréntesis
En primer lugar, mediante la propiedad distributiva quitamos el único paréntesis de la ecuación
Paso 2: quitamos los denominadores de la ecuación de primer grado.
Calculamos el mcm de los denominadores, que es 2, y multiplicamos la ecuación por ese número.
Simplificamos las fracciones de cada término
Paso 3: simplificamos términos semejantes.
Sin embargo, no hay términos semejantes en ninguno de los dos miembros de esta ecuación.
Paso 4: Regla de la suma.
Despejamos la incógnita mediante la regla de la suma. Primero sumamos +24 en los dos miembros de la ecuación:
Paso 5: regla del producto.
Dividimos la ecuación por el coeficiente de la incógnita. En este caso, dividimos entre 3.
Contenido