Probabilidad condicional
La probabilidad condicional es la posibilidad de que ocurra un determinado acontecimiento, dado que otro acontecimiento se produce como condición. Esta información adicional puede (o no) cambiar la percepción de que algo va a suceder.
Por ejemplo, podemos preguntarnos "¿Cuál es la probabilidad de que llueva hoy, dado que no ha llovido en dos días? El evento para el que queremos saber la probabilidad es que llueva hoy, y la información adicional que condicionaría la respuesta es que "no ha llovido en dos días".
Sea un espacio de probabilidad compuesto por Ω (espacio de muestra), ℬ (los eventos aleatorios), y P (la probabilidad de cada evento), más los eventos A y B que pertenecen a ℬ.
La probabilidad condicionada de que A ocurra, dado que B ocurrió, que se denota como P (A│B), se define de esta manera:
P (A│B) = P (A∩B) / P(B) = P (A y B)/P(B)
Dónde: P(A) es la probabilidad de que ocurra A, P(B) es la probabilidad de que ocurra B y es diferente de 0, y P(A∩B) es la probabilidad de la intersección entre A y B, es decir, la probabilidad de que ambos eventos ocurran (probabilidad conjunta).
Se trata de una expresión del teorema de Bayes aplicada a dos eventos, propuesta en 1763 por el teólogo y matemático inglés Thomas Bayes.
Probabilidad condicional ejemplos
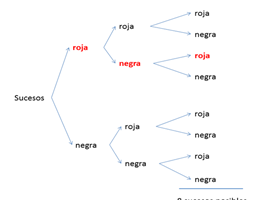
Veamos algunos ejemplos para comprender mejor el concepto de probabilidad condicional:
Calcular la probabilidad de que cuando se tira un dado, salga 3 si se sabe de antemano que ha salido un número impar:
Tenemos que calcular: P(3 | número impar)
P(3|pares) = P(3 ∩ impares) / P(impares)
P(impar) = 3/6 = 1/2
P(3 ∩ impar) = probabilidad de obtener 3 y también impar = 1/6
P(3|par) = (1/6) / (1/2) = 1/3
Otros conceptos estadísticos
- Probabilidad: frecuencia esperada de un fenómeno aleatorio basada en la experiencia
- Población: estos son los elementos que se analizan para realizar los cálculos de probabilidad
- Muestra: estos son los casos de una población estudiada en un estudio probabilístico
- Muestreo: técnicas de obtención de muestras en una población
- Promedio: valor promedio tomado por los eventos de un fenómeno aleatorio
- Moda (Mo) : es el valor más frecuente dado en una muestra de datos
- Mediana (Yo): valor que deja la mitad de los eventos ordenados en cada lado
- Desviación estándar o típica (σ): medición del grado de dispersión de los resultados obtenidos
- Varianza (σ2): se calcula cuadrando la desviación estándar
- Percentiles (Pn): valor del elemento que es mayor que un porcentaje de la muestra
- Deciles (Dn): valor del elemento que es mayor que un porcentaje (tomado por grupos de 10%)
- Cuartiles (Qn): valor del elemento que es mayor que un porcentaje (tomado por grupos de 25%)
- Quintiles (Qn): valor del elemento que es mayor que un porcentaje (tomado por grupos de 20%)
- Variable aleatoria: función que asigna un valor numérico a cada elemento de una muestra aleatoria
- Función de probabilidad: función (P) que asigna a cada valor (xi) una probabilidad (pi)
- Función de distribución: función que indica la probabilidad de obtener un valor ≤ a un evento
- Esperanza matemática: valor medio que se puede esperar de un fenómeno aleatorio
- Distribución binomial: es una distribución de eventos cuya probabilidad es fija
- Distribución normal o gaussiana: distribución que toma valores continuos y no discretos.
Contenido