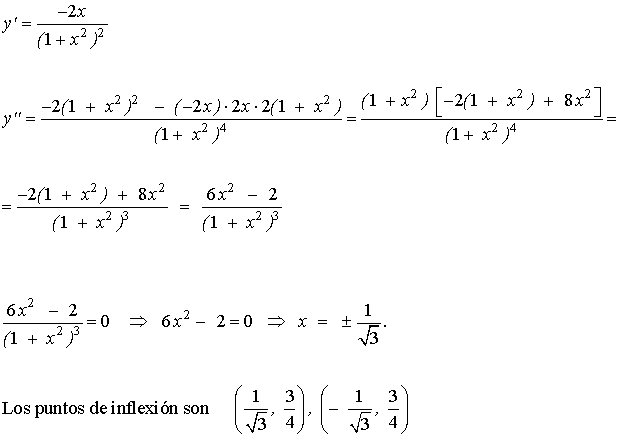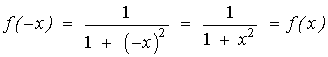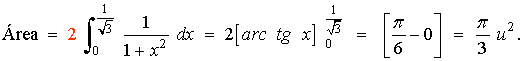La simetría de una función
Como podemos imaginar, las funciones pueden tener diferentes formas y algunas de ellas son simétricas, otras antisimétricas y otras simplemente tienen formas variadas que no presentan ningún tipo de simetría.
Las simetrías siempre dependen de un eje (el espejo donde haríamos la simetría).
Puntos de corte con los ejes
Cuando tenemos que representar una función, muchas veces es muy conveniente saber en qué punto exacto la función corta los dos ejes, el x y el y.
Simetrías de una función
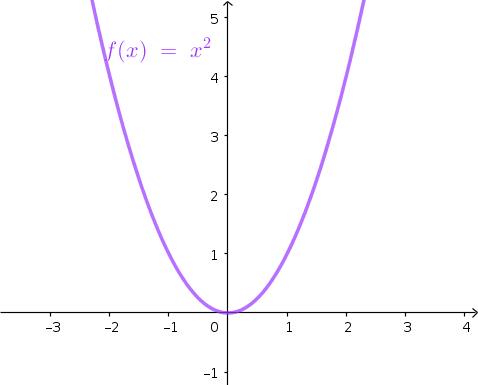
Una función es simétrica con respecto al eje de ordenadas (OY), si por cada valor, x, de su dominio se cumple que
.
En este caso decimos que la función es par. y
son iguales. Por tanto es par
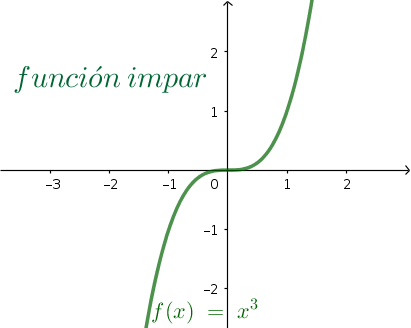
Una función es simétrica con respecto al origen de las ordenadas, si por cada valor, x, de su dominio se cumple que
.
En este caso decimos que la función es impar. y
son iguales, pero de distinto signo. Por tanto es impar.
Ejemplo de Función simétrica
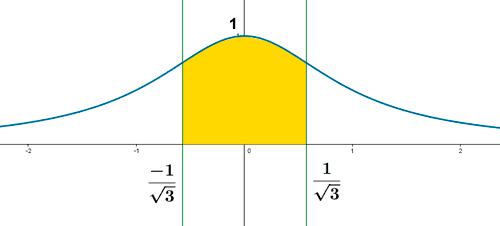
Calcula el área comprendida entre la curva:
el eje OX y las líneas verticales que pasan por los puntos de giro de esa curva.
Empezamos calculando los puntos de giro. Estos puntos serán los que verifiquen que la segunda derivada en ellos es nula.
Observamos ahora que la función es pareja:
Demostramos que la función es simétrica par:
De manera que el área que nos piden puede calcularse como el doble por tener simetría par:
Contenido