El cuadrado
En geometría, se estudian varias figuras, siendo el cuadrado una de ellas. Es una figura plana con cuatro lados que tienen todos la misma medida. También se conoce como un polígono regular que tiene cuatro ángulos de 90º cada uno. Es una figura muy conocida ya que se puede ver en la vida cotidiana ya que muchas de las cosas que usamos a diario tienen una forma cuadrada por lo que es muy popular.
Elementos del cuadrado
El cuadrado está compuesto por diferentes elementos que, colocados de forma correcta, dan la forma y las medidas exactas. Estos elementos son:
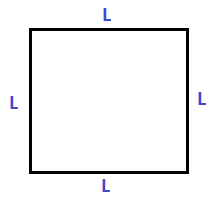
- Los lados: En el cuadrado hay cuatro lados, todos con las mismas medidas o longitudes. Se dice que esta figura es un paralelogramo ya que sus lados son paralelos pero de dos a dos. Están representados por la letra L.
- Los ángulos: En el cuadrado también debe haber cuatro ángulos. Todos ellos deben ser rectos, es decir, deben medir 901 cada uno. No puede ser un cuadrado si uno de sus ángulos no cumple con este elemento pero sería alguna otra figura geométrica.
- Los vértices: Son los puntos donde coinciden los lados. En un cuadrado debe haber cuatro vértices que estén situados exactamente en cada ángulo.
- Las diagonales: Se dice que las diagonales de un cuadrado son las líneas que cruzan el cuadrado porque van de un vértice a otro pero del lado opuesto. Las diagonales están en el centro del cuadrado y debe haber dos por cada figura. Están representadas por la letra D.
Cómo calcular las diagonales de un cuadrado
Para calcular las diagonales de un cuadrado se debe aplicar una fórmula que se obtiene a través del famoso teorema de Pitágoras. Se encuentra justo dentro del triángulo rectángulo que aparece entre dos lados del cuadrado y la diagonal que lo cruza:
D = 2 . l
Lo siguiente que hay que hacer entonces es despejar D por lo que debemos pasar el cuadrado al segundo miembro pero como raíz, de la siguiente manera:
D = l2 + l2
Ahora todos los términos están agrupados pero dentro de la misma raíz:
D = 2l2
Y como paso final procedemos a realizar la raíz de los dos factores y de esta manera la fórmula del principio permanece:
D = 2 . l
La forma correcta de medir las diagonales de un cuadrado es en unidades lineales, de la misma manera que los lados. Es necesario que no sólo se pueda aprender esta fórmula de memoria sino que se conozca todo el proceso. Esto con el fin de ser capaz de aplicarla de la manera correcta. El cálculo de las diagonales de un cuadrado puede ser un procedimiento complejo.
Cómo calcular el área de un cuadrado
El cálculo del área de un cuadrado es un ejercicio muy común que debe conocerse en profundidad. Consiste en multiplicar un lado por otro lado. En otras palabras, lo que hay que hacer es elevar al cuadrado la longitud de un lado y se obtiene el resultado esperado. La fórmula en este caso es la siguiente:
Área = lado x lado = lado2
Puedes, entonces, multiplicar la base por la altura, pero ambas tendrán siempre la misma medida por lo que procedes a multiplicar el mismo lado pero dos veces. La forma correcta de medir el área es en unidades cuadradas.
Cómo calcular el perímetro de un cuadrado
Este es el ejercicio más fácil de resolver ya que la fórmula no es para nada compleja. Así, se dice que el perímetro de un cuadrado viene a ser la suma de todos los lados del cuadrado.
Perímetro = l + l + l + l
En este sentido podemos entender que los lados de un cuadrado tienen la misma medida, entonces lo que se hace es que el perímetro se puede obtener multiplicando la longitud de uno de los lados cuatro veces que es lo mismo que si se sumaran todos los lados. Entonces la fórmula sería:
Perímetro = 4 x lados
La forma correcta de medir el perímetro de un cuadrado es en unidades lineales, de la misma manera que se hace con los lados.
Contenido