Cómo sacar la ecuación de una recta

La idea de una línea recta es uno de los conceptos intuitivos de la Geometría (como también lo son el punto y el plano). La línea puede entenderse como un conjunto infinito de puntos alineados en una sola dirección. Visto en un plano, una línea puede ser horizontal, vertical o diagonal (inclinada a la izquierda o a la derecha).

Ecuación de una recta

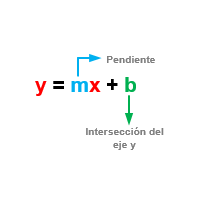
La ecuación principal de una línea se llama expresión de la forma: y = mx +n.

Forma simplificada de la ecuación de la recta

Si se conoce la pendiente m, y el punto donde la línea corta al eje de ordenadas es ( 0, b ) (corresponde a n en la fórmula principal ya vista), podemos deducir, a partir de la ecuación de la línea de la forma

y − y ₁= m(x − x ₁)

y – b = m(x – 0)

y – b = mx

y = mx + b

Se trata de una segunda forma de la ecuación principal de la línea (también se llama forma explícita de la ecuación ) y se utiliza cuando se conoce la pendiente y la ordenada al origen (o intercepción), que llamaremos b (no hay que olvidar que corresponde a n en la primera forma de la ecuación principal). También se puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen de una ecuación dada.

Ejemplo: La ecuación y = 4x + 7 tiene una pendiente 4 y un coeficiente de posición 7, lo que indica que interceptará el eje y en el punto (0, 7) .

Conociendo la fórmula de la ecuación principal (simplificada o explícita, como se quiera llamar) de la línea es posible obtener la ecuación de cualquier línea siempre que se nos den al menos dos variables de la misma: puede ser la pendiente, puede ser un punto o puede ser la intercepción.

Entrada Relacionada: Binomio de newton

Esto significa que si se te da esa información puedes obtener una ecuación de la forma y = mx + b que cumple con esas condiciones dadas. Observa que la ecuación y = mx + b es la forma generalizada de la forma principal y = mx + n; por lo tanto, b corresponde al valor de n (la intercepción en la ordenada y).

Contenido