Cálculo de vectores

Un vector es cualquier segmento de línea dirigido en el espacio. Cada vector tiene algunas características que son Origen o también llamado punto de aplicación. Es el punto exacto sobre el que actúa el vector. El módulo que es la longitud o el tamaño del vector. Para encontrarlo es necesario conocer el origen y el final del vector, ya que para saber cuál es el módulo del vector, debemos medir desde su origen hasta su final. La dirección que viene dada por la orientación en el espacio de la recta que lo contiene. Y la dirección que, mediante una punta de flecha al final del vector, indica hacia qué lado de la línea de acción se dirige el vector.

Magnitudes escalares

Llamamos Magnitudes Escalares a aquellas en las que las mediciones se expresan correctamente mediante un número y la unidad correspondiente. Ejemplos de ello son las siguientes magnitudes, entre otras:

Masa
Temperatura
Presiona
Densidad

Magnitudes de los vectores

Las magnitudes de los vectores son magnitudes que para ser determinadas requieren un valor numérico, una dirección, una dirección y un punto de aplicación.

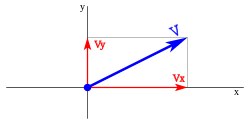
Vector

Un vector es la expresión que proporciona la medida de cualquier magnitud vectorial. Podemos considerarlo como un segmento orientado, en el que podemos distinguir:

Un origen o punto de aplicación: A.
Un final: B.
Una dirección: la de la línea que lo contiene.
Una dirección: indicada por la punta de flecha en B.
Un módulo, que indica la longitud del segmento AB.

Vectores iguales

Dos vectores son iguales cuando tienen el mismo módulo y la misma dirección.

Entrada Relacionada: Ejemplos de factor común

Vector libre

Un vector libre se caracteriza por su módulo, dirección y sentido. El vector libre es independiente de su ubicación.

Suma y resta de vectores

La suma de dos vectores libres es otro vector libre que se determina de la siguiente manera:

El punto de aplicación de uno de ellos se coloca sobre el extremo del otro; el vector de la suma es el vector que tiene su origen en el origen del primero y su extremo en el extremo del segundo.
Por lo tanto, el vector suma de dos vectores coincide con una de las diagonales, la "saliente", del paralelogramo que puede formarse con los vectores suma; la otra diagonal representa la sustracción de estos vectores.
Para hacer sumas o restas de tres o más vectores, el proceso es idéntico. Basta con aplicar la propiedad asociativa.
El vector obtenido mediante la suma o la resta de varios vectores se denomina resultante.

Contenido