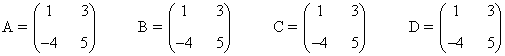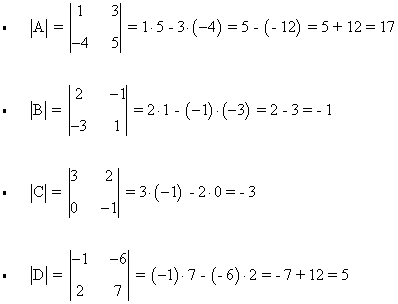Determinantes de tercer orden

Una matriz es un conjunto de elementos de cualquier naturaleza, normalmente números establecidos en filas y columnas. Una matriz de orden «m × n» es un conjunto cuadrangular de componentes dispuestos en m filas y n columnas. El orden de una matriz también se denomina dimensión o tamaño, donde m y n son números naturales.

Determinantes de tercer orden

El determinante es una función que da una matriz de orden n, un único número real llamado el determinante de la matriz. Entonces, si A es una matriz de orden n, el determinante de la matriz A se indicará como det (A) o también puede ser │A│ las barras no simbolizan el valor absoluto.

Para el cálculo de los determinantes de la matriz de cualquier orden, existe una regla que (teorema de Laplace) reduce el cálculo a sumas y restas de varios determinantes de un orden inferior. Este proceso puede repetirse tantas veces como sea necesario hasta que el problema se reduzca al cálculo de múltiples determinantes de un orden tan pequeño como se desee. Sabiendo que el determinante de un escalar es el propio escalar, es posible calcular el determinante de cualquier matriz aplicando este teorema.

La definición de un determinante de la matriz de orden 1, si A=[a] es entonces det(A)=a.

PROPIEDADES DE LOS DETERMINANTES

Los determinantes tienen las siguientes propiedades que son útiles para simplificar su evaluación.

En los párrafos siguientes consideramos que A es una matriz cuadrada.

Propiedad 1

Si una matriz A tiene un renglón (o una columna) de ceros, el determinante de A es cero.

Propiedad 2

El determinante de una matriz A es igual al determinante de la transpuesta de A.

Entrada Relacionada: Ejercicios de circunferencia

Propiedad 3

Si se intercambian dos renglones (o dos columnas) de una matriz A entonces el determinante cambia de signo.

Propiedad 4

Si una matriz A tiene dos renglones (o dos columnas) iguales entonces det A = 0.

Propiedad 5

Cuando un solo renglón (o columna) de una matriz A se multiplica por un escalar r el determinante de la matriz resultante es r veces el determinante de A, r det A.