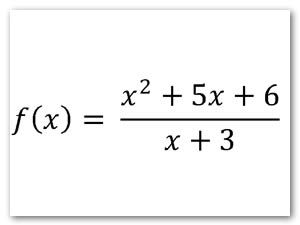
Cómo sacar el dominio de una función
Considere la función que se muestra en el diagrama.
Aquí, el dominio es el conjunto { A , B , C , E }. D no está en el dominio, ya que la función no está definida para D.
El rango es el conjunto {1, 3, 4}. 2 no está en el rango, ya que no hay ninguna letra en el dominio que enlace con 2.
Ejercicios resueltos paso a paso
Ejemplo 1:
Dominio de la función
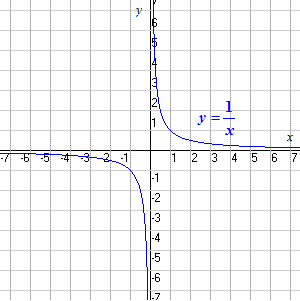
f ( x ) = 1/ x
son todos los números reales excepto el cero (ya que en x = 0, la función no está definida: ¡la división por cero no está permitida!)
El rango es también todos los números reales excepto el cero. Puedes ver que hay algún punto en la curva para cada valor de y, excepto para y = 0.
También se pueden especificar explícitamente los dominios, si hay valores para los que se podría definir la función, pero no queremos considerarlos por alguna razón.
Ejemplo 2:
La siguiente notación muestra que el dominio de la función está restringido al rango (-1, 1).
f ( x ) = x 2 , -1 x 1
El gráfico de esta función es como se muestra. Obsérvense los círculos abiertos, que muestran que la función no está definida en x = -1 y x = 1. De modo que el rango de la función es
0 y < 1.
Contenido