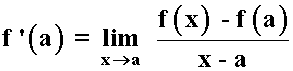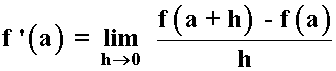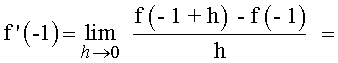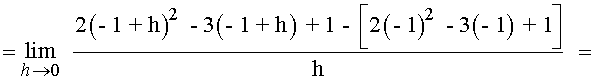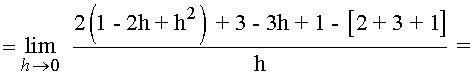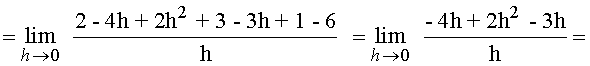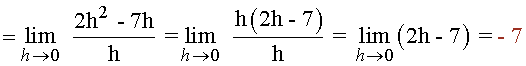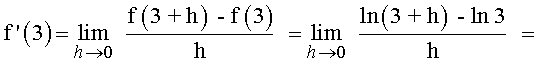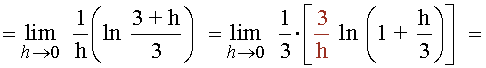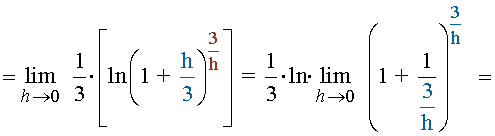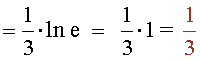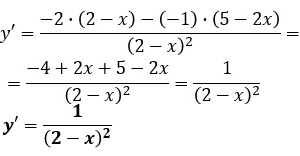Derivada de una función en un punto
La derivada nos sirve para encontrar la pendiente de la recta tangente a una gráfica en un punto x dado.
La derivada de una función en un punto mide la velocidad a la que varía el valor de la función en dicho punto al cambiar el valor de la variable independiente X.
La derivada nos da respuesta a preguntas de este estilo:
¿A qué velocidad está cambiando esto? ,¿a qué velocidad estamos conduciendo justo ahora?, ¿a qué velocidad se estará extendiendo la mancha de petróleo del petrolero accidentado al cabo de una semana?
La derivada de la posición de un coche con respecto al tiempo es su velocidad.
Si en la definición hacemos x = a + h la fórmula quedaría de la siguiente forma:
Ejemplos de Derivada de una función en un punto
Contenido