Inecuaciones con dos incógnitas

Un sistema de desigualdades lineales con dos incógnitas es un conjunto de dos o más de estas desigualdades. El par (s1,s2) es la solución del sistema si satisface todas las desigualdades simultáneamente. La región de solución, si existe, también se denomina región factible.

Inecuaciones

Primero tenemos que representar la línea obtenida al cambiar la desigualdad de la desigualdad por una igual.
Observación: Cuando la desigualdad no tiene el término en x, es una línea horizontal, paralela al eje OX. Cuando el caso es el contrario, es decir, es la desconocida y la que no aparece, es una línea vertical, es decir, paralela al eje OY.
La línea divide el plano en dos partes, según la desigualdad, debemos elegir una u otra. Para ello, una forma práctica es elegir un punto del plano que no pertenezca a la línea (siempre que sea posible el (0,0) es el más fácil), sustituimos en nuestra desigualdad y, si se cumple, elegimos la región del plano donde está el punto; en caso contrario, elegimos la parte opuesta.

Ejemplo de Inecuaciones

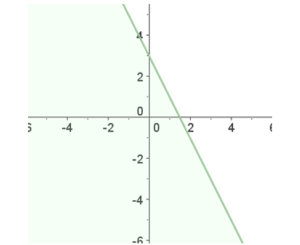
Resolver la siguiente desigualdad con dos incógnitas: 2x+y ≤ 3

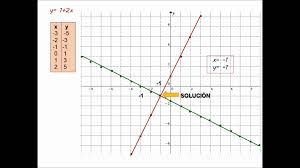
Lo transformamos en una igualdad: 2x +y = 3, y hacemos una tabla de valores o simplemente damos valores para representar la línea:

- Si x=0, entonces y=3 → (0, 3)
- Si x=1, encones y=1 → (1, 1)

Elegimos una región del plano, para ello sustituimos por el punto (0,0) en la desigualdad principal: 2∙0+0 ≤ 3 → 0 ≤ 3. Como el 0 es menor o igual a 3, entonces, elegimos la región donde está nuestro punto.

Entrada Relacionada: Proyecciones matemáticas

Inecuaciones con dos incógnitas

En primer lugar, de manera análoga al caso en el que sólo teníamos una incógnita, resolvemos cada inequidad por separado, aunque en el mismo plano.
Finalmente, elegimos la parte del plano donde ambas soluciones coinciden. Puede ser que no haya ninguna solución.

Ejemplo de Inecuaciones con dos incógnitas

Resolver el siguiente sistema de desigualdades con dos incógnitas:

Resolvemos las desigualdades por separado:

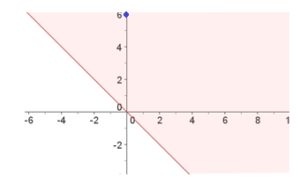
1ª desigualdad: x+y ≥ 0 → x+y =0,
-Si x=0, entonces y= 0 → (0,0)
-Si x=1, entonces y= -1 → (1, -1)

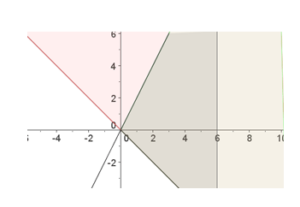
Representamos la línea y elegimos una parte. Ahora tenemos que elegir otro punto ya que el (0,0) pertenece a nuestra línea. Sea por ejemplo el (0,6), 0+6 ≥ 0 →6 ≥ 0. Como se cumple tomaremos la parte donde el punto es (0,6)

2ª desigualdad: 2x-y ≥ 0 → 2x-y =0
-Si x=0, entonces y= 0 → (0,0)
-Si x=1, entonces y= 2 → (1, 2)

Elegimos, como en el caso anterior el (0,6), entonces: 2∙0-6 ≥ 0 → -6 ≥ 0. Como no se cumple, elegimos la parte opuesta.

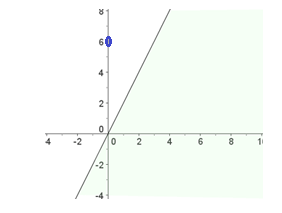
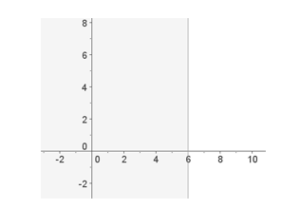
3ª desigualdad: x ≤ 6 → x=6, como hemos comentado al principio, es una línea vertical, que toma todos los valores menores de 6, es decir, a la izquierda de 6:

2º. Finalmente, nuestra solución será la parte en la que coincidan todas las soluciones, será la parte que quede coloreada con un color más intenso: