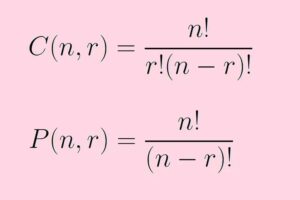Ejercicios de variaciones

Las variaciones no repetitivas u ordinarias, Vm, n son los diferentes grupos de m elementos diferentes tomados de n en n (m > n).

Combinaciones, variaciones y permutaciones

Para aplicar la Regla de Laplace, el cálculo de los acontecimientos favorables y los posibles acontecimientos a veces no plantea ningún problema, ya que son un número pequeño y pueden ser fácilmente calculados:

Por ejemplo: La probabilidad de que cuando se tira un dado, salga el número 2. Sólo hay un caso favorable, mientras que los casos posibles son seis.

Probabilidad de coincidir con el horóscopo de una persona en el primer intento. Hay un caso favorable y 12 casos posibles.

Sin embargo, a veces el cálculo del número de casos favorables y posibles casos es complejo y hay que aplicar reglas matemáticas:

Por ejemplo: 5 parejas casadas se sientan al azar en la cena y queremos calcular la probabilidad de que al menos los miembros de un matrimonio se sienten juntos. En este caso, determinar el número de casos favorables y posibles casos es complejo.

Las reglas matemáticas que pueden ayudarnos son el cálculo de combinaciones, el cálculo de variaciones y el cálculo de permutaciones.

Combinaciones

Determina el número de subgrupos de 1, 2, 3, etc. elementos que pueden formarse con los "n" elementos de uno de los nuestros. Cada subgrupo es diferente del resto en los elementos que lo componen, sin la influencia del orden.

Por ejemplo, calcula las posibles combinaciones de 2 elementos que se pueden formar con los números 1, 2 y 3.

Puedes establecer 3 pares diferentes: (1,2), (1,3) y (2,3). Al calcular las combinaciones, los pares (1,2) y (2,1) se consideran idénticos, por lo que sólo se cuentan una vez.

Entrada Relacionada: Límite infinito entre infinito

Variaciones

Calcular el número de subgrupos de 1, 2, 3, etc. elementos que pueden establecerse con los "n" elementos de una muestra. Cada subgrupo se diferencia del resto por los elementos que lo componen o por el orden de esos elementos (esto es lo que lo diferencia de las combinaciones).

Por ejemplo, calcula las posibles variaciones de 2 elementos que se pueden establecer con los números 1, 2 y 3.

Ahora tendríamos 6 pares posibles: (1,2), (1,3), (2,1), (2,3), (3,1) y (3,3). En este caso los subgrupos (1,2) y (2,1) se consideran diferentes.

Permutaciones

Calcula las posibles agrupaciones que se pueden establecer con todos los elementos de un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el orden de los elementos.