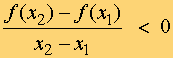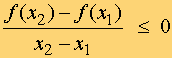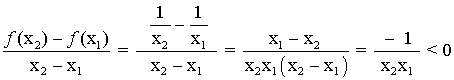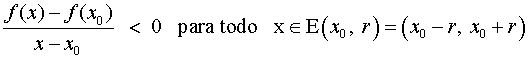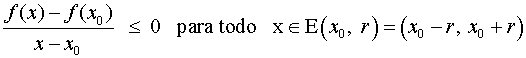Monotonía de una función
Una función f(x) es estrictamente decreciente en un intervalo (a, b) si para dos valores cualesquiera del intervalo x1 y x2 tales que x1 < x2 , se cumple que f(x1) > f(x2) .
Decir que f(x1) > f(x2) es lo mismo que :
Será creciente si f(x1) ≥ f(x2) , es decir:
Una función es decreciente si al aumentar la 'x' disminuye la 'y' .
Ejemplo de función estrictamente creciente
f(x) = 1/x
Es estrictamente decreciente en [0 , ∞) , ya que para dos puntos cualesquiera x1 y x2 en dicho intervalo obtenemos que:
Ya que el denominador es siempre positivo.
Es estrictamente decreciente en [-∞ , 0] . La demostración es la misma que en el caso anterior.
Decrecimiento de una función en un punto
Una función f(x) es estrictamente decreciente en un punto de abscisa x0 si existe un entorno simétrico de x0 en el que la función es estrictamente decreciente. Es decir:
Una función f(x) es decreciente en un punto de abscisa x0 si existe un entorno simétrico de x0 en el que la función es decreciente. Es decir:
Ejemplo de crecimiento y decrecimiento de una función
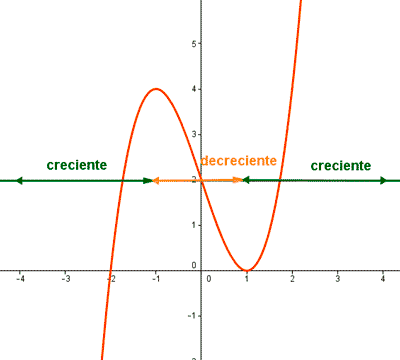
Determinar los intervalos de crecimiento y decrecimiento de la función:
f(x) = x3 - 3x + 2
• (-∞ , - 1): la función es estrictamente creciente.
Es decir, al aumentar la x, aumenta la y .
• (- 1 , 1): la función es estrictamente decreciente.
Es decir, al aumentar la x, disminuye la y .
• (1 , ∞): la función es estrictamente creciente.
Es decir, al aumentar la x, aumenta la y .
Contenido