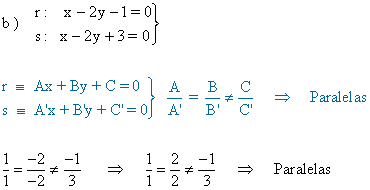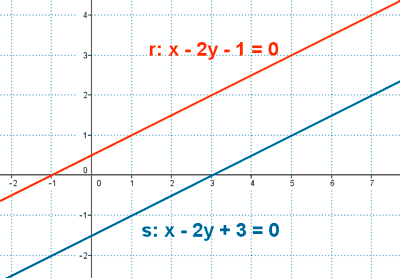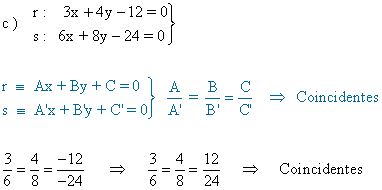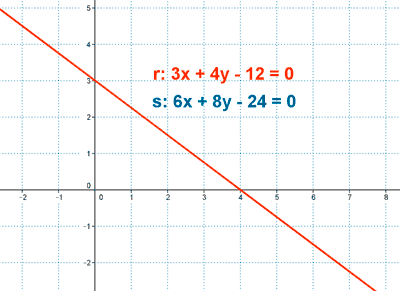Posición relativa de dos rectas
Sólo hay dos posiciones relativas entre un punto y una línea: El punto está en la línea, es decir, si compruebas la ecuación de la línea. En este caso se dice que el punto está en la línea. El punto no está en la línea, es decir, no comprueba la ecuación de la línea.
Posición relativa de dos rectas
Dos líneas del plano pueden ocupar una de las tres posiciones siguientes:
- Secantes: Se cortan en un punto.
- Paralelas: No están cortadas.
- Coincidencia: Tienen infinitos puntos en común, son la misma línea.
ejercicio
Procedimiento
Para determinar la posición relativa de dos líneas podemos usar
Resuelve el sistema formado por las dos ecuaciones y dependiendo del número de soluciones del sistema que tengamos:
- 1 solución: Las líneas son secantes.
- 0 soluciones: Las líneas son paralelas.
- Infinitas soluciones: Las líneas son coincidentes.
Compare las pendientes y la ordenada en el origen de cada línea:
- Diferentes pendientes: Las líneas son secantes.
- Misma pendiente y diferente orden en el origen: Las líneas son paralelas.
- Misma pendiente y orden igual en el origen: Las líneas son coincidentes.
Ejemplo de Posición relativa de dos rectas
Contenido