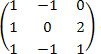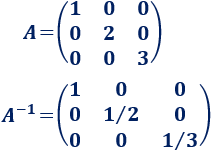
Matriz inversa por gauss jordan
Dada una matriz A, ¿podemos encontrar otra matriz B tal que A-B=B-A=I? Esta matriz B existe aunque no siempre, si existe se llama matriz inversa de A y se denota A-1. Para que exista la inversa de A, tiene que ser cuadrada, de lo contrario el producto no podría hacerse por la izquierda y la derecha, entonces cuando hablamos de matrices invertibles estamos hablando de matrices cuadradas.
Matriz inversa por gauss jordan
Método de Gauss-Jordan
Este método consiste en colocar junto a la matriz de partida (A) la matriz de identidad (I) y realizar operaciones por filas, que afectan tanto a A como a I, para transformar la matriz A en la matriz de identidad, la matriz resultante de las operaciones sobre I es la inversa de A(A-1).
Las operaciones que podemos hacer en las filas son:
a) Sustituir una fila por ella multiplicada por una constante, por ejemplo, sustituimos la fila 2 por ella multiplicada por 3.
b) Sustituir dos filas
c) Sustituir una fila por una combinación lineal de ella y otras.
La matriz inversa de A es
A través de la matriz de adjuntos
Dada una matriz A, determinamos la matriz adjunta de su transposición. Si multiplicamos esa matriz por 1/|A| obtenemos la matriz inversa de A.
Contenido