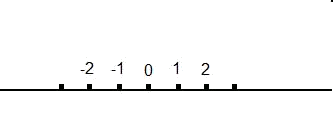Números complejos
Un número complejo es un par ordenado de números (reales, imaginarios). Estos pueden ser representados por la letra z, como sigue:
z = (a, b)
Donde el primer componente se llama parte real y se escribe D; el segundo se llama parte imaginaria y se escribe Im.
- a es la parte real Re(z).
- b es la parte imaginaria Im(z).
NÚMEROS COMPLEJOS EN FORMA DE BINOMIO
Llamamos al número a + bi un número complejo en forma de binomio, donde a es la parte real y b es la parte imaginaria.
- Si b = 0, el número complejo se reduce a uno real porque a + 0i = a.
- Si a = 0, el número complejo se reduce a bi y se dice que es un número imaginario puro.
NÚMEROS COMPLEJOS CONJUGADOS
Los números complejos z = a + bi y z = a - bi se llaman conjugados.
Ejemplo: z1 = (4, -5) es el conjugado de z2 = (4, 5).
NÚMEROS COMPLEJOS OPUESTOS
Los números complejos a + bi y - (a + bi) se llaman opuestos.
Ejemplo: z3 = 5 + 7i es el opuesto de z4 = - 5 - 7i.
LA IGUALDAD DE LOS NÚMEROS COMPLEJOS
Dos números complejos son iguales cuando tienen el mismo componente real y el mismo componente imaginario.
Representación de números complejos en el plano
Ahora que sabemos cómo trabajar con números complejos y las operaciones básicas de suma, resta, multiplicación y división, entremos en la representación de estos números en el plano complejo. Para los números reales, dibujaríamos una línea y los colocaríamos de forma ordenada, es decir:
Para representar gráficamente un número complejo, debemos dibujarlos en el plano complejo. Éste está formado por un eje real y un eje imaginario. En el eje real representaremos la parte real del número complejo, mientras que en el eje imaginario representaremos la parte imaginaria. Estos ejes se dibujarán perpendiculares y secantes en el cero, que no tiene parte real e imaginaria.
Contenido