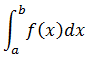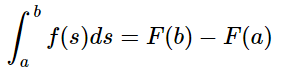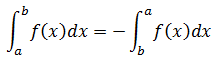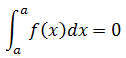
Integral definida
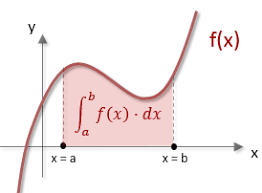
Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre el gráfico de f(x), el eje de las abscisas y las líneas verticales x = a y x = b.
La integral definida es uno de los conceptos fundamentales del Análisis Matemático.
La integral definida de f(x) en el intervalo [a,b] es igual al área limitada entre el gráfico de f(x), el eje de las abscisas y las líneas verticales x = a y x = b (bajo la hipótesis de que la función f es positiva). Esta integral se representa por:
a es el límite inferior de la integración y b es el límite superior de la integración
Si la función F es una función primitiva de f en el intervalo [a,b], por la Regla de Barrow tienes que:
Las propiedades de la integral definida
El valor de la integral definida cambia de signo si se modifican los límites de integración.
Si los límites de integración coinciden, la integral definida vale cero.
Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].
La integral definida de una suma de funciones es igual a la suma de integrales...
El producto integral de una constante por una función es igual a la constante por la integral de la función.
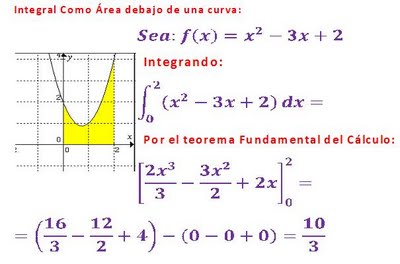
Integral definida ejercicios resueltos
La imagen de ejemplo tiene un error en el primer término, al integrar x^2 es x^3/3, luego al reemplazar 2 en x, es 8/3, siendo el resultado 2/3.
Contenido