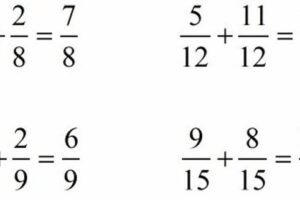Operaciones con fracciones
Al igual que con otros tipos de números, con el uso de fracciones también es posible realizar operaciones básicas, como la suma, la resta y la multiplicación. Cada una de ellas tiene un método que debe seguirse para su resolución, que dependerá en gran medida del tipo de fracciones utilizadas en las diferentes operaciones.
Suma de fracciones
Para realizar la suma de las fracciones, primero se debe verificar si sus denominadores son iguales o diferentes. Si los denominadores son los mismos, se procede a la suma de los numeradores y se coloca el mismo denominador, de la siguiente manera
Por otra parte, si los denominadores de las fracciones a sumar son diferentes, se debe colocar un denominador común, lo que se logra calculando el mínimo común múltiplo (m.c.m.) de ambos denominadores. Por ejemplo, dada la suma de fracciones:
El mínimo común múltiplo de 3 y 5 es 15. Por lo tanto, el nuevo denominador de ambas fracciones es el número 15. El resultado de esta operación es obtener el valor de los nuevos numeradores que acompañarán al denominador común calculado anteriormente.
- Para la primera fracción (5/3): 15 ∕ 3= 5
5 × 5= 25 - Para la segunda fracción (4/5): 15 ∕ 5= 3
3 × 4= 12
Así, las nuevas fracciones a resolver serían 25/15 y 12/15; y la suma de ambas se resuelve como una suma de fracciones con denominadores iguales mencionadas anteriormente. El resultado de la operación de la suma de estas fracciones es:
Sustracción de fracciones
Como sucede con la suma de fracciones, para restar dos fracciones deben tener el mismo denominador; en tal caso, que las dos fracciones a restar tengan el mismo denominador, la operación se resuelve restando los numeradores y colocando el mismo denominador; de la siguiente manera:
Por otra parte, cuando las fracciones no tienen el mismo denominador, deben ser transformadas; para ello se calcula el mínimo común múltiplo (m.c.m.) de ambos denominadores, obteniendo así el nuevo común denominador para ambas fracciones.
El mínimo común múltiplo de 6 y 4 es 12, por lo tanto, el común denominador de las nuevas fracciones será el número 12. Entonces, los nuevos numeradores que acompañarán a este denominador deben ser calculados para realizar la operación; para ello, el nuevo denominador se divide por el antiguo denominador, luego este resultado se multiplica por el numerador.
- Para la primera fracción (8/6): 12 ∕ 6= 2
2 × 8= 16 - Para la segunda fracción (2/4): 12 ∕ 4= 3
3 × 2= 6
De esta manera se obtienen las nuevas fracciones 16/12 y 6/12, que se resolverán como una resta de fracciones con los mismos denominadores. El resultado de esta operación es el siguiente:
Multiplicación de fracciones
Para hacer multiplicaciones de fracciones, se deben multiplicar las numeradas (sean iguales o diferentes), el número resultante será el numerador de la fracción final; luego, se multiplican los denominadores (sean iguales o diferentes) y así mismo, el resultado de esta operación será el denominador de la fracción final. Finalmente, la fracción resultante puede simplificarse, si es el caso.
Para que sirven las fracciones
Utilizamos fracciones todos los días, aunque a veces no nos damos cuenta, pero son de vital importancia en la vida cotidiana.
Por ejemplo, si pedimos medio kilo de plátanos o un cuarto de mandarinas, estamos usando las fracciones, ya que estamos dividiendo el kilo en mitades o cuartos.
Contenido
