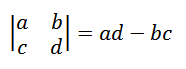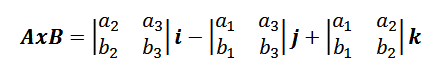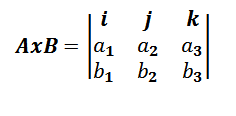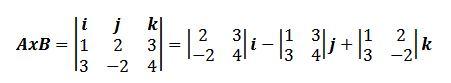Producto cruz
El producto vectorial, que también se llama producto cruzado o producto exterior, tiene diferentes propiedades algebraicas y geométricas. Estas propiedades son muy útiles, especialmente en el estudio de la física.
Una definición formal del producto vectorial es la siguiente: si A = (a1, a2, a3) y B = (b1, b2, b3) son vectores, entonces el producto vectorial de A y B, que denominaremos AxB, es:
AxB = (a2b3 - a3b2 , a3b1 - a1b3 , a1b2 - a2b1)
Debido a la notación AxB, se lee como "A cruz B".
Un ejemplo de cómo utilizar el producto externo es que si A = (1, 2, 3) y B = (3, -2, 4) son vectores, entonces utilizando la definición de producto vectorial que tenemos:
AxB = (1, 2, 3) x (3, -2, 4) = (2*4 - 3*(-2), 3*3 - 1*4, 1*(-2) - 2*3 )
AxB= (8 + 6 ,9 - 4, - 2 - 6) = (14, 5, - 8).
Otra forma de expresar el producto vectorial viene dada por la notación de los determinantes.
El cálculo de un determinante de segundo orden viene dado por:
Por lo tanto, la fórmula del producto vectorial dada en la definición puede ser reescrita como sigue:
Esta suele simplificarse en un determinante de tercer orden de la siguiente manera:
Donde i, j, k representan los vectores que forman la base de R3.
Usando esta forma de expresar el producto cruz, tenemos que el ejemplo anterior lo podemos reescribir como:
Producto cruz ejercicios resueltos
Obtener una ecuación del plano que pasa por los puntos P(1, 3, 2), Q(3, – 2, 2) y R(2, 1, 3).
Sea A= QR = (2 – 3,1 + 2, 3 – 2) y B = PR = (2 – 1,1 – 3, 3 – 2). Entonces A = – i + 3j + k y B = i – 2j + k. Para encontrar el plano formado por esos tres puntos basta con encontrar un vector que sea normal al plano, el cual es AxB.
AxB = (– i + 3j + k)x( i – 2j + k) = 5i +2j – k.
Con este vector, y tomando al punto P(1, 3, 2), podemos determinar la ecuación del plano como sigue:
(5, 2,– 1)∙(x – 1,y – 3,z – 2) = 5(x – 1) + 2(y – 3) – (z – 2) = 0
Así, tenemos que la ecuación del plano es 5x + 2y – z – 9 = 0.