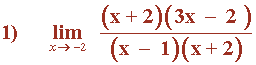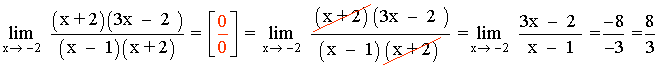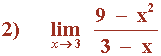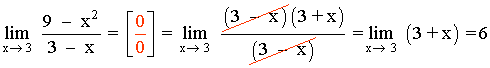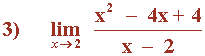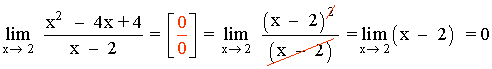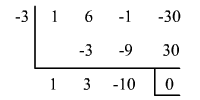Límite tiende a cero
Ese límite puede ser +∞, -∞ o, simplemente, sin límite.
Veremos en los ejemplos expuestos que en los límites donde k / 0 se alcanza (donde k es una constante), el valor al que tiende la x no existe en el dominio de la función. La función no está definida en ese punto.
La operación consiste en comprobar los límites laterales. Si nos acercamos mucho al límite de la izquierda y, a su vez, al de la derecha, veremos que en el numerador tenemos un número, positivo o negativo, y en el denominador un número más cercano a cero, que también puede ser positivo o negativo. Dependiendo de los signos, el resultado de ambos límites laterales puede ser +∞ o -∞. Si ambos límites laterales coinciden, el límite existe (es una condición necesaria para la existencia de cualquier límite en un punto).
Por el contrario, si uno de los límites laterales da +∞ y el otro -∞, el límite no existe.
Este último sería el caso de asíntotas verticales divergentes.
Ejemplos de Límite tiende a cero
Hallar los siguientes límites factorizando el numerador y denominador de la función:
Contenido