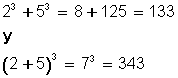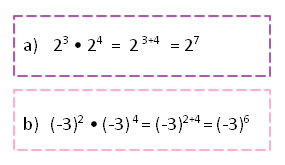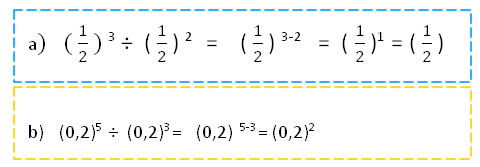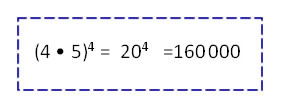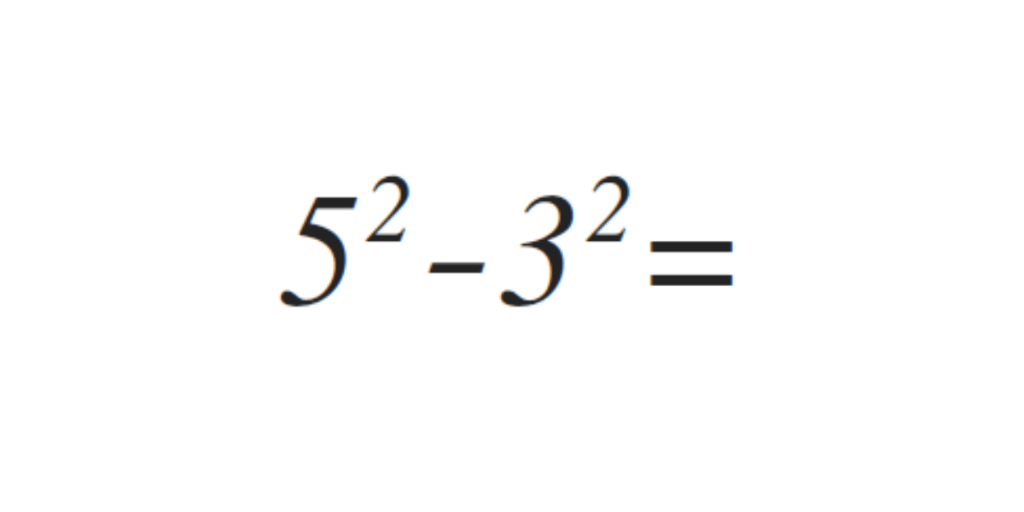
Suma y resta de potencias
Por otra parte, cuando la potencia se combina con la adición o la sustracción, se realizan diferentes operaciones y no se pueden aplicar las propiedades de las potencias vistas hasta ahora.
Por ejemplo:
Si se quieren sumar dos potencias de igual base:
La forma más simple y directa de realizar estas operaciones es simplemente calcular primero las potencias y luego sumarlas.
Se observa que esta operación indica lo siguiente:
(10 x 10 x 10 x 10) + (10 x 10 x 10) = 10.000 + 1.000 = 11.000
donde se expresan dos operaciones: la suma y el producto.
Así que la expresión más simple para la operación anterior es
como está escrito al principio.
Otro caso en el que hay que tener cuidado es en la suma de poderes como el siguiente:
Es muy importante convencerse para siempre de que
La manera más segura de convencerse es calculando ambas operaciones:
Es evidente, entonces, que ya que
(133 es distinto a 343).
Esto significa que los poderes no son distributivos con respecto a la suma y la diferencia.
Multiplicación de potencias
El producto de las potencias de igual base es igual a la misma base elevada a la suma de los exponentes.
ap • aq = a p+q
Ejemplo:
División de potencias de igual base
El cociente de potencias de igual base es igual a la misma base elevada a la resta de los exponentes.
an : am = an-m
Ejemplos:
Obsérvese que el resultado de dividir dos potencias de igual base es otra potencia con la misma base, y donde el exponente es la resta de los exponentes iniciales.
Multiplicación de potencias de igual exponente
Para obtener el producto de potencias de igual exponente, debemos multiplicar las bases y mantener el exponente.
ap • bp= (a • b)p
Ejemplo:
44 • 54 =
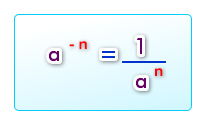
Para multiplicar las potencias con el mismo exponente negativo, se aplica el mismo procedimiento anterior y se conserva el signo del exponente. Una potencia con exponente negativo y base diferente de cero, es igual a una fracción con numerador 1 y con denominador igual a la potencia con exponente positivo:
Contenido