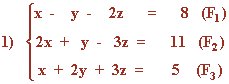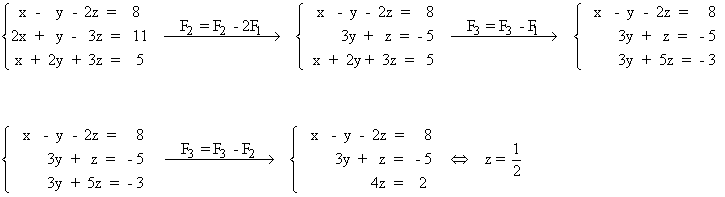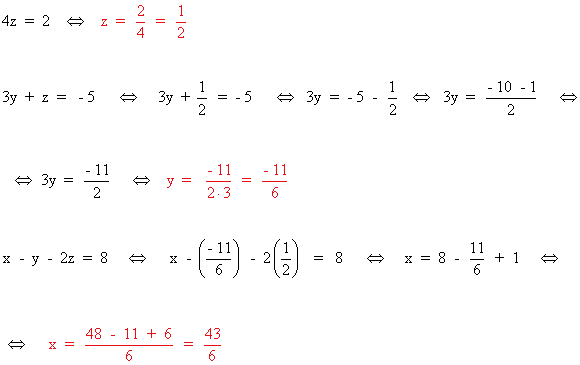Ejercicios de sistemas de ecuaciones 3x3

Se llama ecuación lineal con tres incógnitas la suma de las tres incógnitas, multiplicada por números, e igualando la suma a otro número (las incógnitas no pueden elevarse a exponentes ni multiplicarse entre sí) Se llama solución de la ecuación lineal a un conjunto de valores que al sustituirlos en las incógnitas hacen que la igualdad se verifique.

Resolver un sistema de tres variables

Al igual que cuando se resuelven sistemas de dos ecuaciones, hay tres posibles resultados para la solución de un sistema de tres variables. Vamos a estudiar esto visualmente, aunque no vamos a graficar estas ecuaciones.

Caso 1: Existe una solución. Para que tres ecuaciones con tres variables tengan una solución, los planos deben ser interceptados en un solo punto.
Caso 2: No hay solución. Los tres planos no tienen ningún punto en común. (Obsérvese que dos ecuaciones podrían tener puntos en común entre sí, pero no con las tres). A continuación se presentan ejemplos de algunas formas en que esto sucede.
Caso 3: Hay un número infinito de soluciones. Esto sucede cuando los tres planos se intersectan en una línea. Y también puede suceder cuando los tres planos están en el mismo plano.

Pasos para resolver un sistema de ecuaciones lineales de 3x3

Elija una variable y límpiela en una de las ecuaciones

Normalmente se elige la variable con el coeficiente más bajo, y de la ecuación más simple, para que el despeje no requiera tanto trabajo algebraico.

Sustituir en las otras dos ecuaciones

Usa este espacio para sustituir esta variable en las otras dos ecuaciones. Las dos nuevas ecuaciones que resulten de este paso formarán un sistema de ecuaciones de 2x2.

Entrada Relacionada: Resolución de multiplicaciones y divisiones con números enteros

Resolver el sistema 2x2

Para ello repito el proceso:

Elijo una de las 2 variables y la convierto en una de las ecuaciones.
Utilizo este despeje para sustituir la variable en la otra ecuación (la que no despejé en el sistema 2x2).
Del paso anterior obtendré una ecuación lineal de una variable, que cuando la despeje, obtendré su valor.
El valor que obtuve lo sustituyo en el despeje que hice en este sistema 2x2, y así calcularé el valor de otra variable.

Obtengo el valor de la variable que me falta

Como con el paso 3 obtuve el valor de dos de las tres variables, para obtener la que faltaba utilizo el claro que hice en el paso 1 y lo sustituyo por las incógnitas que ya he resuelto.