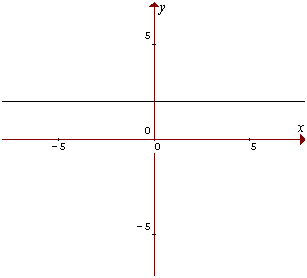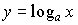Funciones elementales
Una función elemental es aquella que puede construirse a partir de una cantidad finita de exponenciales, logaritmos, constantes, una variable, raíces de ecuaciones a través de la composición y las combinaciones, utilizando las cuatro operaciones elementales que serían, la suma, la resta, la multiplicación y la división. Las funciones trigonométricas y sus inversas se encuentran dentro del grupo de funciones elementales ya que se pueden obtener mediante el uso de variables complejas y sus relaciones entre las funciones trigonométricas, las funciones exponenciales y el logaritmo. Un ejemplo de una función que no es elemental es la función de error. Esta función se utiliza en el campo de la probabilidad, la estadística y las ecuaciones diferenciales parciales.
Funciones elementales
En matemáticas, una función elemental es una función construida a partir de un número finito de exponenciales, logaritmos, constantes, variables y raíces de ecuaciones por composición y combinaciones utilizando las cuatro operaciones elementales (+ - × ÷). Las funciones trigonométricas y sus inversas se consideran dentro del grupo de funciones elementales, ya que pueden obtenerse utilizando variables complejas y sus relaciones entre las funciones trigonométricas y las funciones exponenciales y logarítmicas.
Gráficas de las Funciones Elementales
Constante:
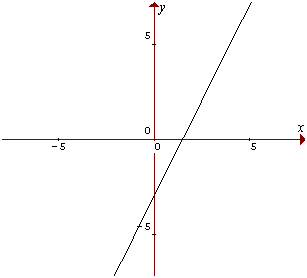
Recta:
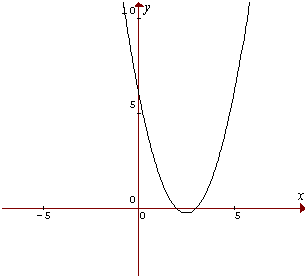
Cuadrática:
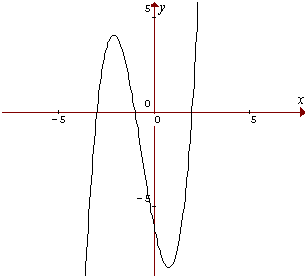
Polinómica de grado 3:
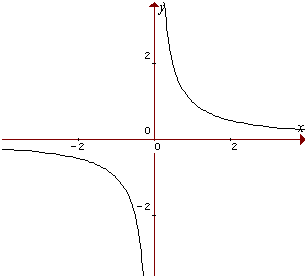
Proporcionalidad Inversa:
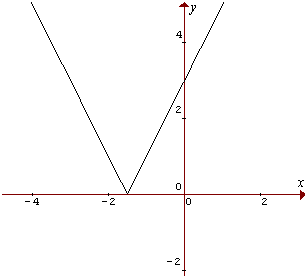
Valor Absoluto de 1º grado:
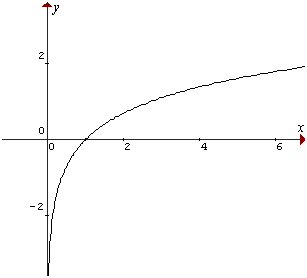
Logarítmica:
Contenido