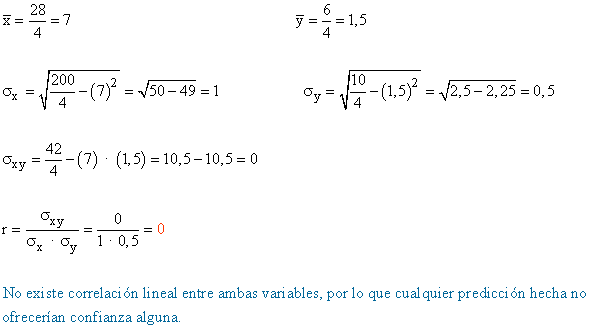Estadísticas descriptivas
El coeficiente de correlación de Pearson es un tipo de coeficiente utilizado en las estadísticas descriptivas. En concreto, se utiliza en la estadística descriptiva aplicada al estudio de dos variables.
Por otra parte, la estadística descriptiva (también llamada análisis exploratorio de datos) agrupa un conjunto de técnicas matemáticas destinadas a obtener, organizar, presentar y describir un conjunto de datos, con el fin de facilitar su utilización. En general, utiliza como soporte tablas, medidas numéricas o gráficos.
El coeficiente de correlación de Pearson: ¿para qué sirve?
El coeficiente de correlación de Pearson se utiliza para estudiar la relación (o correlación) entre dos variables aleatorias cuantitativas (escala de intervalo mínimo); por ejemplo, la relación entre peso y altura.
Es una medida que nos da información sobre la intensidad y la dirección de la relación. En otras palabras, es un índice que mide el grado de covarianza entre diferentes variables linealmente relacionadas.
Debemos tener clara la diferencia entre relación, correlación o covariación entre dos variables (= variación conjunta) y causalidad (también llamada pronóstico, predicción o regresión), ya que son conceptos diferentes.
¿Cómo se interpreta?
El coeficiente de correlación de Pearson comprende valores entre -1 y +1. Por lo tanto, dependiendo de su valor, tendrá un significado u otro.
Si el coeficiente de correlación de Pearson es igual a 1 o -1, podemos considerar que la correlación que existe entre las variables estudiadas es perfecta.
Si el coeficiente es mayor que 0, la correlación es positiva ("A más, más y menos"). En cambio, si es menor que 0 (negativo), la correlación es negativa ("A más, menos, y a menos, más). Por último, si el coeficiente es igual a 0, sólo podemos afirmar que no existe una relación lineal entre las variables, pero puede haber algún otro tipo de relación.
Consideraciones
El coeficiente de correlación de Pearson aumenta si la variabilidad de X y/o Y (las variables) aumenta, y disminuye en el caso contrario. Por otra parte, para afirmar si un valor es alto o bajo, debemos comparar nuestros datos con otras investigaciones con las mismas variables y en circunstancias similares.
Para representar las relaciones de diferentes variables que se combinan linealmente, podemos utilizar la llamada matriz de varianza-covarianza o la matriz de correlación; en la diagonal de la primera encontraremos valores de la varianza, y en la de la segunda encontraremos unos (la correlación de una variable consigo misma es perfecta, =1).
Coeficiente al cuadrado
Cuando cuadramos el coeficiente de correlación de Pearson, su significado cambia, e interpretamos su valor en relación con las predicciones (indicando la causalidad de la relación).
Coeficiente de correlación de pearson ejercicios resueltos
Una persona rellena semanalmente una quiniela y un boleto de lotería primitiva, anotando el número de aciertos que tiene. Durante las 4 semanas del mes de febrero, los aciertos fueron :
| Semana | 1ª | 2ª | 3ª | 4ª |
|---|---|---|---|---|
| Aciertos en la quiniela | 6 | 8 | 6 | 8 |
| Aciertos en la primitiva | 1 | 2 | 2 | 1 |
Obtener el coeficiente de correlación lineal e interpretarlo. ¿Ofrecerían confianza las predicciones hechas con las rectas de regresión?
| xi | yi | xi2 | yi2 | xi · yi |
|---|---|---|---|---|
| 6 | 1 | 36 | 1 | 6 |
| 8 | 2 | 64 | 4 | 16 |
| 6 | 2 | 36 | 4 | 12 |
| 8 | 1 | 64 | 1 | 8 |
| 28 | 6 | 200 | 10 | 42 |
Contenido