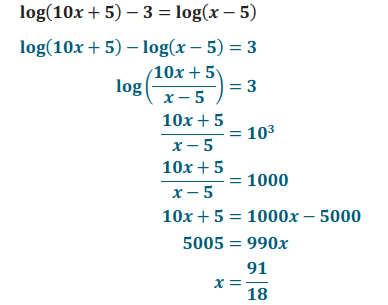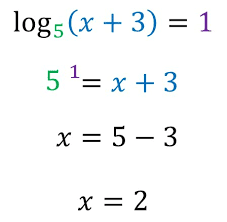
Cómo resolver ecuaciones logarítmicas
Una ecuación logarítmica es una ecuación cuya incógnita (o desconocida) se encuentra multiplicando o dividiendo los logaritmos, en sus bases o en el argumento de los logaritmos (dentro de los logaritmos).
Cómo resolver ecuaciones logarítmicas
Ecuaciones logaritmicas en la que todos sus elementos son logaritmos:
Los pasos son los siguientes:
- Determinar si el problema sólo contiene logaritmos. Si es así, vaya al paso 2. Si no, deténgase y utilice los pasos para resolver ecuaciones logarítmicas que contengan términos sin logaritmos.
- Utilice las propiedades de los logaritmos para simplificar el problema si es necesario. Si el problema tiene más de un logaritmo a cada lado del signo igual, entonces el problema puede simplificarse para dejar sólo un término logarítmico en cada lado.
- Reescribir la ecuación sin logaritmos.
- Simplifique la ecuación si es necesario.
- Borrar lo desconocido o la variable.
Ecuaciones logarítmicas que tienen términos no logarítmicos
Los pasos son los siguientes:
- Determinar si el problema sólo contiene logaritmos. Si es así, deténgase y utilice los pasos para resolver las ecuaciones logarítmicas que sólo contienen logaritmos. Si no es así, vaya al Paso 2.
- Utilice las propiedades de los logaritmos para simplificar el problema si es necesario. Si el problema tiene más de un logaritmo a cada lado del signo igual, entonces el problema puede ser simplificado.
- Reescriba el problema exponencialmente.
- Simplificar la ecuación si es necesario.
- Borrar la variable.
- Revisar la solución. Recuerda que no podemos tomar el logaritmo de un número negativo, por lo que debemos asegurarnos de que cuando reinsertamos la solución en la ecuación original obtenemos un número positivo. De lo contrario, debemos descartar esta solución.
Ejemplos de cómo resolver ecuaciones logarítmicas
Contenido