Blog

Cómo resolver una integral definida

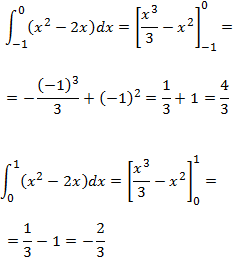
Cómo resolver una integral definida
Se llama primitiva de la función f(x) en un intervalo (a, b) cualquier función F(x) diferenciable en (a, b) y tal que F′(x) = f(x).

Integral Definida

Desde su origen, la noción de integral ha respondido a la necesidad de mejorar los métodos de medición de las áreas subtendidas bajo líneas y superficies curvas. La técnica de integración se desarrolló principalmente a partir del siglo XVII, en paralelo con los avances que tuvieron lugar en las teorías sobre las derivadas y en el cálculo diferencial.

Concepto de integral definida

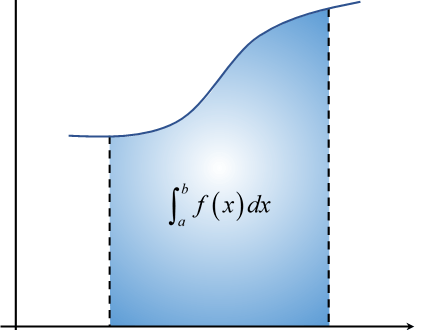
La integral definida es un concepto utilizado para determinar el valor de las áreas limitadas por curvas y líneas rectas. Dado el intervalo [a, b] en el que para cada uno de sus puntos x se define una función f (x) mayor o igual a 0 en [a, b], la integral definida de la función entre los puntos a y b se denomina área de la porción del plano limitada por la función, el eje horizontal OX y las rectas verticales de las ecuaciones x = a y x = b.

La integral definida de la función entre los extremos del intervalo [a, b] se denomina

Propiedades de la integral definida

La integral definida tiene las siguientes propiedades:

  • Cada integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
  • Cuando la función f (x) es mayor que cero, su integral es positiva; si la función es menor que cero, su integral es negativa.
  • La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
  • La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, es posible "sacar" la constante de la integral).
  • Al permitir los límites de una integral, cambia su signo.
  • Dados tres puntos de tal manera que a < b < c, entonces se cumple que (integración a las piezas):
  • Para cualquier punto x del intervalo [a,b] al que se aplican dos funciones f (x) y g (x) de manera que f (x) £ g (x), se verifica que

Regla de barrow

Aplicar la Regla de Barrow para calcular las integrales definidas de x2-2x en los intervalos [-1, 0]
y  [0,1]:

Entradas Relacionadas